/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite

Zadanie nr 3561396

Dodaj do ulubionych
Dodaj do rozwiązanych

Rzucamy dwa razy sześcienną kostką do gry. Oblicz prawdopodobieństwo wyrzucenia dwa razy nieparzystej liczby oczek, jeżeli wiadomo, że pięć oczek nie wypadło ani razu.

Rozwiązanie

Ustalmy, że za zdarzenia elementarne przyjmujemy pary otrzymanych wyników.

Sposób I

Skoro wiemy, że pięć oczek nie wypadło, to możemy myśleć, że mamy kostkę, która ma 5 ścianek (nie ma tej z piątką). Zatem

|Ω | = 5 ⋅5.

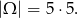
Mamy teraz na każdej kostce 2 liczby nieparzyste (1 i 3), zatem jest

2 ⋅2

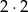
zdarzeń sprzyjających. Zatem prawdopodobieństwo wynosi

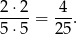
2⋅ 2 4 ---- = ---. 5⋅ 5 25

Sposób II

Zadanie możemy też rozwiązać ze wzoru na prawdopodobieństwo warunkowe:

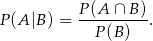
P (A |B ) = P-(A-∩-B-). P(B )

Tym razem myślimy o normalnych kostkach, czyli

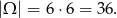
|Ω | = 6 ⋅6 = 36 .

Ponadto 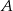A to zdarzenie otrzymania dwóch liczb nieparzystych, a 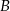B zdarzenie, że na żadnej kostce nie ma piątki. Mamy zatem

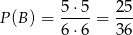
5 ⋅5 25 P(B ) = ---- = --- 6 ⋅6 36

(bo na każdej kostce mamy 5 możliwości).

Zdarzenia 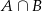A ∩ B to takie, że mamy dwie liczby nieparzyste, ale nie ma wśród nich 5, czyli

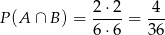
2 ⋅2 4 P(A ∩ B ) = ---- = --- 6 ⋅6 36

(bo na każdej kostce mamy 2 możliwości). Zatem

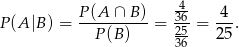
4- P(A |B) = P-(A-∩-B-) = -36= -4-. P(B ) 2356 25

 
Odpowiedź: -4 25

Wersja PDF