Zadanie nr 4483495
W dwóch urnach znajdują się kule białe i czarne, przy czym w pierwszej jest 6 kul białych i 4 czarne, a w drugiej urnie 5 białych i 5 czarnych. Rzucamy raz symetryczną kostką do gry. Jeżeli wyrzucimy co najmniej 4 oczka to losujemy 2 kule z pierwszej urny, a jeżeli wyrzucimy co najwyżej 3 oczka to losujemy 2 kule z drugiej urny. Oblicz prawdopodobieństwo wylosowania dwóch kul białych.
Rozwiązanie
Po pierwsze zauważmy, że wyrzucenie ’co najmniej 4 oczek’ i wyrzucenie ’co najwyżej 3 oczek’ są jednakowo prawdopodobne, czyli każdą z urn wybieramy z prawdopodobieństwem 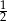 .
.
Policzmy jakie jest prawdopodobieństwo wylosowania dwóch kul białych w każdej z urn. W obu urnach znajduje się 10 kul, więc w każdym przypadku jest tyle samo zdarzeń elementarnych.

Policzmy zdarzenia sprzyjające, jest ich odpowiednio
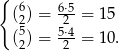
Pozostało skorzystać ze wzoru na prawdopodobieństwo całkowite (lub z drzewka jak ktoś woli):
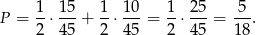
Odpowiedź: