/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite

Zadanie nr 5034027

Zestaw tematów egzaminacyjnych składa się z 15 tematów z algebry, 15 z geometrii i n tematów z prawdopodobieństwa. Z zestawu usunięto jeden temat, a następnie wylosowano z pozostałych jeden temat. Oblicz n , jeśli wiadomo, że prawdopodobieństwo wylosowania tematu z prawdopodobieństwa wynosi 1 4 .

Wersja PDF

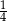Rozwiązanie

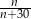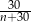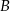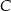Mamy dwie możliwości: albo przy pierwszym losowaniu usunięto temat z prawdopodobieństwa (tak mogło się zdarzyć z prawdopodobieństwem n+n30- ), albo usunięto inny temat (tak mogło się zdarzyć z prawdopodobieństwem --30- n+ 30 ). Oznaczmy te zdarzenia przez B i C . Za to przez 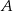A oznaczmy zdarzenie wylosowania w drugim losowaniu tematu z prawdopodobieństwa. Wiemy, że 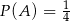1 P (A) = 4 . Z drugiej strony ze wzoru na prawdopodobieństwo całkowite (lub ze zdrowego rozsądku, lub z drzewka) mamy

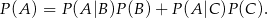
P (A ) = P(A |B)P (B) + P (A |C )P(C ).

Policzmy występujące w tym wzorze prawdopodobieństwa warunkowe.

n-−--1- P(A |B) = n + 29 n P(A |C) = -------. n + 29

O tych równościach trzeba myśleć tak: jaka jest szansa zajścia 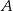A jeżeli wiemy, że zaszło B (lub C).

Mamy zatem równanie

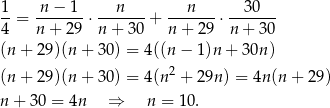
1 n− 1 n n 30 --= -------⋅ -------+ -------⋅ ------- 4 n + 29 n+ 30 n + 2 9 n+ 30 (n + 29)(n + 30) = 4((n − 1)n + 3 0n) 2 (n + 29)(n + 30) = 4(n + 29n ) = 4n(n + 29) n + 30 = 4n ⇒ n = 10.

 
Odpowiedź: n = 10

Wersja PDF