Zadanie nr 5205552
Janek przeprowadza doświadczenie losowe, w którym jako wynik może otrzymać jedną z liczb: 0, 1, 2, 3, 4, 5, 6. Prawdopodobieństwo 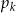 otrzymania liczby
otrzymania liczby 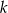 jest dane wzorem:
jest dane wzorem: 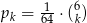 . Rozważamy dwa zdarzenia:
. Rozważamy dwa zdarzenia:
– zdarzenie 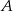 polegające na otrzymaniu liczby ze zbioru
polegające na otrzymaniu liczby ze zbioru 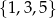 ,
,
– zdarzenie 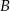 polegające na otrzymaniu liczby ze zbioru
polegające na otrzymaniu liczby ze zbioru 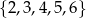 .
.
Oblicz prawdopodobieństwo warunkowe 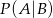
Rozwiązanie
Ze wzoru na prawdopodobieństwo warunkowe mamy
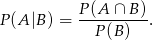
Zdarzenie 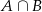 to zdarzenie polegające na otrzymaniu 3-ki lub 5-ki, więc
to zdarzenie polegające na otrzymaniu 3-ki lub 5-ki, więc
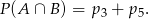
Zauważmy, że zdarzenie 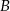 jest przeciwne do zdarzenia polegającego na otrzymaniu 1-ki lub zera, więc
jest przeciwne do zdarzenia polegającego na otrzymaniu 1-ki lub zera, więc
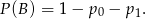
Widać teraz, że musimy obliczyć 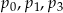 i
i 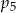 . Można to łatwo zrobić z trójkąta Pascala, albo wprost ze wzoru na symbol Newtona – my wybierzemy tę drugą drogę.
. Można to łatwo zrobić z trójkąta Pascala, albo wprost ze wzoru na symbol Newtona – my wybierzemy tę drugą drogę.
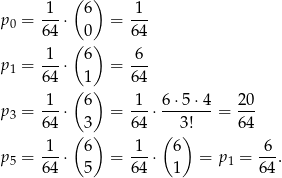
Interesujące nas prawdopodobieństwo jest więc równe
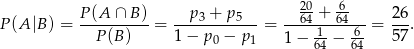
Odpowiedź: