Zadanie nr 6406314

Mamy dwie talie kart po 24 karty. Z pierwszej talii losujemy jedną kartę i nie oglądając jej wkładamy do drugiej talii. Następnie z drugiej talii losujemy jedną kartę.

Jakie jest prawdopodobieństwo wylosowania króla, jeżeli wiemy, że z pierwszej talii przełożono do drugiej treﬂa?
Obliczyć prawdopodobieństwo, że wylosowana karta jest kierem.
Wylosowana karta okazała się kierem. Jakie jest prawdopodobieństwo tego, że z pierwszej talii także został wylosowany kier?

Wersja PDF

Rozwiązanie

Sposób I

Jeżeli przełożyliśmy z pierwszej talii króla treﬂ (co może się zdarzyć z prawdopodobieństwem 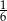), to prawdopodobieństwo wylosowania króla z drugiej talii wynosi 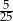. Jeżeli natomiast został przełożony inny treﬂ (co się zdarza z prawdopodobieństwem ), to prawdopodobieństwo wyciągnięcia króla wynosi 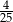. Szukane prawdopodobieństwo jest więc równe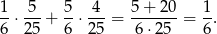

$1 5 5 4 5+ 20 1 --⋅---+ -⋅ ---= -------= -. 6 25 6 25 6 ⋅25 6$

Sposób II

O losowaniu karty z drugiej talii można myśleć jak o dwóch prawdopodobieństwach warunkowych: losujemy pod warunkiem, że karta pochodzi z oryginalnych 24 kart w tej talii, oraz losujemy pod warunkiem, że karta będzie dołożoną kartą. Ponieważ oba prawdopodobieństwa są równe 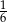, ze wzoru na prawdopodobieństwo całkowite, szukane prawdopodobieństwo też jest równe .
Odpowiedź: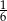
Sposób I

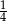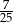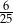Jeżeli przełożyliśmy z pierwszej talii kiera (co może się zdarzyć z prawdopodobieństwem ), to prawdopodobieństwo wylosowania kiera z drugiej talii wynosi . Jeżeli natomiast została przełożona karta w innym kolorze (co się zdarza z prawdopodobieństwem ), to prawdopodobieństwo wyciągnięcia kiera wynosi . Szukane prawdopodobieństwo jest więc równe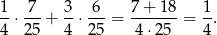

$1-⋅-7-+ 3⋅ 6--= 7+--18-= 1. 4 25 4 25 4 ⋅25 4$

Sposób II

O losowaniu karty z drugiej talii można myśleć jak o dwóch prawdopodobieństwach warunkowych: losujemy pod warunkiem, że karta pochodzi z oryginalnych 24 kart w tej talii, oraz losujemy pod warunkiem, że karta będzie dołożoną kartą. Ponieważ oba prawdopodobieństwa są równe 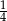, ze wzoru na prawdopodobieństwo całkowite, szukane prawdopodobieństwo też jest równe .
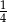Odpowiedź: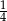
Niech 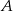będzie zdarzeniem polegającym na wyciągnięciu kiera z pierwszej talii, a 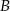na wyciągnięciu kiera z drugiej talii. Musimy policzyć 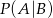. Zanim to zrobimy zauważmy, że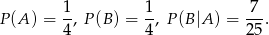
$1- 1- 7-- P (A) = 4, P(B ) = 4, P(B |A ) = 25.$

Korzystamy teraz ze wzoru Bayesa:

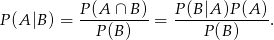
$P(A |B) = P(A-∩--B)-= P(B-|A-)P-(A)-. P(B ) P(B )$

Mamy więc

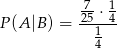
$7 1 -25-⋅4- P (A |B ) = 1 4$

Odpowiedź: