/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite

Zadanie nr 7417418

Dodaj do ulubionych
Dodaj do rozwiązanych

W pierwszej urnie są kule czarne i białe, w drugiej 10 kul niebieskich i 15 kul zielonych, a w trzeciej – 14 kul niebieskich i 7 zielonych. Najpierw losujemy kulę z pierwszej urny, a następnie losujemy kulę z drugiej albo z trzeciej urny w zależności od tego, czy z pierwszej urny wylosowaliśmy odpowiednio kulę białą, czy czarną. Oblicz prawdopodobieństwo wylosowania czarnej kuli z pierwszej urny, jeżeli prawdopodobieństwo wylosowania według opisanego schematu kuli niebieskiej jest takie samo jak zielonej.

Rozwiązanie

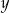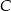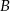Oznaczmy przez x i y liczby odpowiednio kul czarnych i białych w pierwszej urnie, a przez C i B odpowiednio zdarzenia polegające na wylosowaniu kuli czarnej i białej z pierwszej urny. Mamy więc

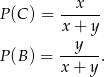
P(C ) = --x--- x + y --y--- P(B ) = x + y .

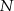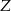Niech N i Z oznaczają zdarzenia polegające na wylosowaniu odpowiednio kuli niebieskiej i zielonej. Mamy zatem (ze wzoru na prawdopodobieństwo całkowite)

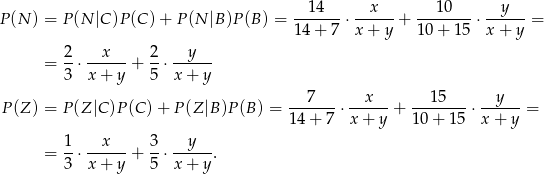
14 x 1 0 y P(N ) = P (N |C)P (C) + P (N |B )P(B ) = -------⋅------+ --------⋅------= 14 + 7 x + y 10 + 15 x + y 2 x 2 y = -⋅ ------+ --⋅ ------ 3 x + y 5 x+ y P (Z) = P (Z |C )P(C )+ P(Z |B)P (B) = ---7---⋅ --x---+ ---15---⋅ --y---= 1 4+ 7 x+ y 10 + 15 x+ y 1 x 3 y = -⋅ ------+ --⋅ -----. 3 x + y 5 x+ y

Wiemy, że 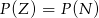P(Z ) = P (N ) , więc

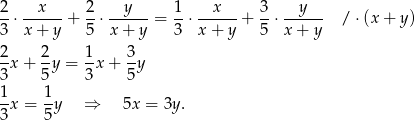
2 x 2 y 1 x 3 y -⋅ ------+ --⋅ ------= -⋅ ------+ --⋅------ / ⋅(x + y) 3 x + y 5 x+ y 3 x+ y 5 x + y 2- 2- 1- 3- 3x + 5 y = 3 x+ 5y 1 1 -x = -y ⇒ 5x = 3y. 3 5

Interesujące nas prawdopodobieństwo jest więc równe

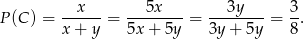
x 5x 3y 3 P (C) = ------= --------= --------= -. x+ y 5x+ 5y 3y+ 5y 8

 
Odpowiedź: 3 8

Wersja PDF