/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite

Zadanie nr 7925094

Dodaj do ulubionych
Dodaj do rozwiązanych

Dane są dwie urny z kulami. W każdej z urn jest siedem kul. W pierwszej urnie są trzy kule czarne i cztery kule białe, w drugiej urnie są dwie kule czarne i pięć białych. Rzucamy jeden raz symetryczną monetą. Jeżeli wypadnie reszka, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – jedną kulę z drugiej urny. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tym doświadczeniu wylosujemy kulę białą.

Rozwiązanie

Szkicujemy urny.

PIC

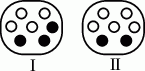
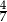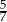Prawdopodobieństwa wylosowania białej kuli z pierwszej i drugiej urny są odpowiednio równe 47 i 57 . Mamy jednak do czynienia z prawdopodobieństwem warunkowym – najpierw musimy wylosować urnę.

Sposób I

Rysujemy drzewko opisujące możliwe zdarzenia.

PIC

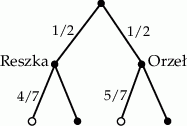
Odczytujemy z drzewka prawdopodobieństwo wylosowania kuli białej.

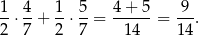
1 4 1 5 4 + 5 9 --⋅ -+ --⋅--= ------= --. 2 7 2 7 1 4 14

Sposób II

Niech 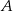A oznacza interesujące nas zdarzenie wylosowania białej kuli, a 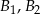B1,B2 niech będą zdarzeniami wylosowania odpowiednio pierwszej i drugiej urny. Korzystamy ze wzoru na prawdopodobieństwo całkowite.

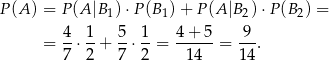
P (A ) = P(A |B1) ⋅P(B 1)+ P (A |B 2)⋅P (B2) = 4 1 5 1 4 + 5 9 = --⋅--+ -⋅ --= ------= ---. 7 2 7 2 14 14

 
Odpowiedź: -9 14

Wersja PDF