/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite

Zadanie nr 8066770

Dodaj do ulubionych
Dodaj do rozwiązanych

Każda z urn oznaczonych liczbami 1, 2, 3 zawiera po 3 kule czarne i 4 białe, a każda urna oznaczona liczbami 4, 5, 6 zawiera po 3 czarne i 2 białe kule. Rzucamy sześcienną kostką do gry, a następnie z urny o numerze równym liczbie wyrzuconych oczek losujemy bez zwracania 2 kule. Co jest bardziej prawdopodobne: wylosowanie dwóch kul czarnych, czy dwóch kul białych?

Rozwiązanie

Zauważmy, że jest jednakowo prawdopodobne, że kule będziemy wyciągać z urn 1, 2, 3, jak to, że będziemy je wyciągać z urn 4, 5, 6. Ponadto, dwie kule czarne lub dwie kule białe możemy wybrać z pierwszych trzech urn z odpowiednio z prawdopodobieństwami

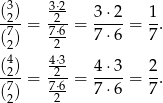
(3) 3⋅2- 3⋅2 1 -27- = -27⋅6-= ----= --. (2) 2 7⋅6 7 (4) 4⋅3- -2- = -2- = 4⋅3-= 2-. (72) 7⋅26- 7⋅6 7

Dla urn 4, 5, 6 prawdopodobieństwa te są odpowiednio równe

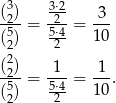
(32) 3⋅22- 3 -5- = 5⋅4-= --- (2) 2 10 (2) 1 1 -25- = 5⋅4-= --. (2) -2- 10

Liczymy teraz kolejno prawdopodobieństwa wylosowania dwóch kul czarnych i dwóch kul białych (korzystamy ze wzoru na prawdopodobieństwo całkowite lub z drzewka).

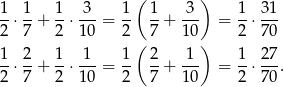
( ) 1 1 1 3 1 1 3 1 3 1 -⋅ --+ --⋅--- = -- --+ --- = --⋅--- 2 7 2 1 0 2 ( 7 10) 2 7 0 1- 2- 1- -1- 1- 2- 1-- 1- 2-7 2 ⋅ 7 + 2 ⋅1 0 = 2 7 + 10 = 2 ⋅7 0.

Widać więc wyraźnie, że prawdopodobieństwo wybrania dwóch kul czarnych jest większe.  
Odpowiedź: Wylosowanie dwóch kul czarnych jest bardziej prawdopodobne.

Wersja PDF