Zadanie nr 9281682
W dwóch pudełkach umieszczono po pięć kul, przy czym w pierwszym pudełku: 2 kule białe i 3 kule czerwone, a w drugim pudełku: 1 kulę białą i 4 kule czerwone. Z pierwszego pudełka losujemy jedną kulę i bez oglądania wkładamy ją do drugiego pudełka. Następnie losujemy jedną kulę z drugiego pudełka. Oblicz prawdopodobieństwo wylosowania kuli białej z drugiego pudełka.
Rozwiązanie
Prawdopodobieństwo wylosowania białej kuli z pierwszej urny jest równe  i w tej sytuacji białe kule stanowią
i w tej sytuacji białe kule stanowią 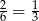 kul w drugim pudełku. Czerwoną kulę możemy natomiast wylosować z pierwszego pudełka z prawdopodobieństwem
kul w drugim pudełku. Czerwoną kulę możemy natomiast wylosować z pierwszego pudełka z prawdopodobieństwem 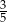 i wtedy białe kule stanowią
i wtedy białe kule stanowią 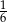 kul w drugim pudełku. Ze wzoru na prawdopodobieństwo całkowite interesujące nas prawdopodobieństwo jest więc równe
kul w drugim pudełku. Ze wzoru na prawdopodobieństwo całkowite interesujące nas prawdopodobieństwo jest więc równe
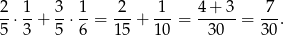
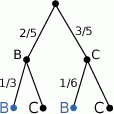
Możemy też tę sytuację przedstawić na drzewku.
Odpowiedź: