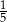Zadanie nr 9542067
Ze zbioru wszystkich liczb naturalnych czterocyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 15, jeśli wiadomo, że jest ona podzielna przez 18.
Rozwiązanie
Wiemy, że wylosowana liczba dzieli się przez 3 (bo dzieli się przez 18), więc podzielność przez 15 sprowadza się do podzielności przez 5.
Sposób I
Ustalmy najpierw ile jest liczb czterocyfrowych podzielnych przez 18. Są to liczby
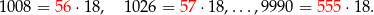
Jest więc 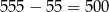 takich liczb.
takich liczb.
Ile spośród tych liczb dzieli się przez 5? – są to liczby podzielne przez 90, czyli liczby
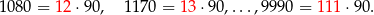
Jest ich więc 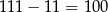 i interesujące nas prawdopodobieństwo jest równe
i interesujące nas prawdopodobieństwo jest równe
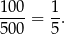
Sposób II
Jeżeli oznaczymy przez 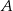 i
i 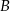 zdarzenia polegające na wylosowaniu liczby czterocyfrowej podzielnej odpowiednio przez 15 i 18, to musimy obliczyć prawdopodobieństwo warunkowe
zdarzenia polegające na wylosowaniu liczby czterocyfrowej podzielnej odpowiednio przez 15 i 18, to musimy obliczyć prawdopodobieństwo warunkowe
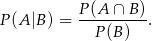
Liczby czterocyfrowe podzielne przez 18 tworzą skończony ciąg arytmetyczny  o różnicy
o różnicy 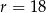 i taki, że
i taki, że
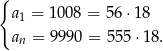
Mamy stąd
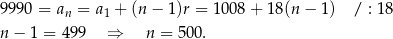
Zatem
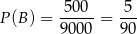
(bo wszystkich liczb czterocyfrowych jest  ).
).
Zajmijmy się teraz zdarzeniem  , czyli liczbami, które są jednocześnie podzielne przez 15 i 18. Takie liczby to dokładnie liczby podzielne przez 90. Tworzą one skończony ciąg arytmetyczny
, czyli liczbami, które są jednocześnie podzielne przez 15 i 18. Takie liczby to dokładnie liczby podzielne przez 90. Tworzą one skończony ciąg arytmetyczny 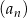 o różnicy
o różnicy 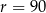 i taki, że
i taki, że
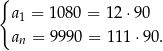
Mamy stąd
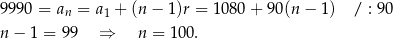
Zatem
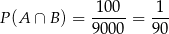
i interesujące nas prawdopodobieństwo jest równe
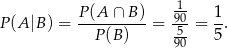
Odpowiedź: