Zadanie nr 9810986
Z talii 52 kart losujemy jednocześnie dwie karty. Oblicz prawdopodobieństwo, że przynajmniej jedna z nich będzie starsza od 10, jeśli wiadomo, że żadna z nich nie jest karem.
Rozwiązanie
Sposób I
Skoro wiemy, że wśród wylosowanych kart nie ma kara, to tak naprawdę losujemy z 39 kart bez kara. Przyjmując, że wyniki to nieuporządkowane pary wylosowanych kart, mamy
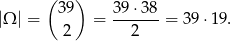
Zdarzenia sprzyjające to takie, że co najmniej jedna karta jest większa 10. Możemy te zdarzenia podzielić na dwa zbiory: takie, gdy obie karty są większe od 10 i takie, gdy tylko jedna z nich. Takich zdarzeń jest odpowiednio
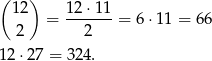
Zatem szukane prawdopodobieństwo wynosi
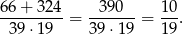
Sposób II
Oznaczmy przez 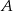 zdarzenie polegające na tym, że wśród dwóch wylosowanych kart przynajmniej jedna jest starsza od 10, a przez
zdarzenie polegające na tym, że wśród dwóch wylosowanych kart przynajmniej jedna jest starsza od 10, a przez 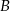 , że żadna z nich nie jest karem. Musimy policzyć prawdopodobieństwo warunkowe
, że żadna z nich nie jest karem. Musimy policzyć prawdopodobieństwo warunkowe
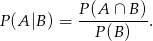
Przyjmijmy, że zdarzenia elementarne to nieuporządkowane pary wylosowanych kart. Zatem
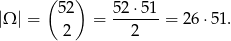
Łatwo policzyć zdarzenia sprzyjające do 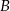 to są wszystkie pary bez kara, jest ich zatem
to są wszystkie pary bez kara, jest ich zatem
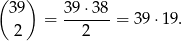
Zatem
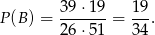
Zdarzenia sprzyjające do 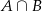 to takie, że żadna karta nie jest karem i co najmniej jedna jest starsza od 10. Możemy rozdzielić takie zdarzenia na takie, gdy obie karty są większe od 10 i takie gdy tylko jedna jest większa od 10. Daje to nam
to takie, że żadna karta nie jest karem i co najmniej jedna jest starsza od 10. Możemy rozdzielić takie zdarzenia na takie, gdy obie karty są większe od 10 i takie gdy tylko jedna jest większa od 10. Daje to nam
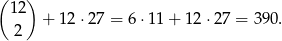
Zatem
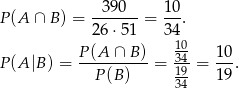
Odpowiedź: