Zadanie nr 5928397
W okrąg o równaniu 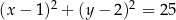 wpisano trójkąt
wpisano trójkąt 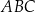 . Bok
. Bok 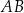 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu 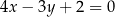 . Wysokość
. Wysokość 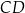 tego trójkąta dzieli bok
tego trójkąta dzieli bok 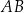 tak, że
tak, że 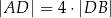 . Oblicz pole trójkąta
. Oblicz pole trójkąta 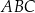 .
.
Rozwiązanie
Dany okrąg to okrąg o środku 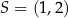 i promieniu
i promieniu 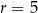 . Szkicujemy opisaną sytuację.
. Szkicujemy opisaną sytuację.
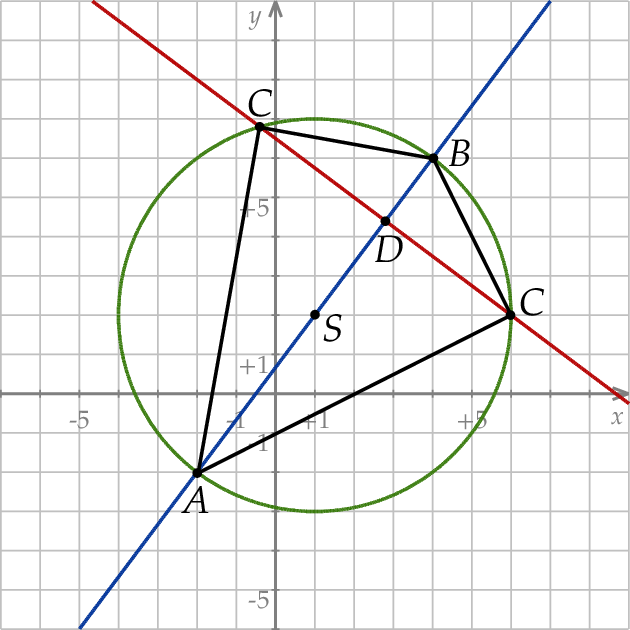
Sposób I
Jeżeli w miarę dokładnie wykonamy rysunek, to możemy nabrać podejrzeń, że dana prosta 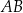 przechodzi przez środek
przechodzi przez środek 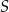 danego okręgu. Łatwo sprawdzić, że faktycznie tak jest – wystarczy podstawić współrzędne punktu
danego okręgu. Łatwo sprawdzić, że faktycznie tak jest – wystarczy podstawić współrzędne punktu 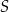 do równania prostej:
do równania prostej:
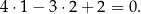
W szczególności, odcinek 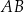 jest średnicą okręgu, czyli
jest średnicą okręgu, czyli
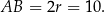
Wiemy też, że punkt 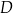 dzieli odcinek
dzieli odcinek  w stosunku 4:1, więc
w stosunku 4:1, więc
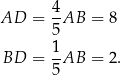
Kąt 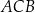 jako kąt oparty na średnicy jest prosty (są dwa możliwe położenia punktów
jako kąt oparty na średnicy jest prosty (są dwa możliwe położenia punktów 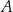 i
i 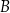 i są cztery możliwe położenia punktu
i są cztery możliwe położenia punktu  , ale nie ma to wpływu na samo rozwiązanie), więc trójkąt
, ale nie ma to wpływu na samo rozwiązanie), więc trójkąt 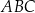 jest prostokątny, a
jest prostokątny, a 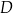 jest spodkiem wysokości opuszczonej na przeciwprostokątną. Korzystamy teraz ze znanego faktu, że ta wysokość jest średnią geometryczną długości odcinków, na które podzieliła przeciwprostokątną. Mamy zatem
jest spodkiem wysokości opuszczonej na przeciwprostokątną. Korzystamy teraz ze znanego faktu, że ta wysokość jest średnią geometryczną długości odcinków, na które podzieliła przeciwprostokątną. Mamy zatem
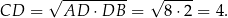
Pole trójkąta 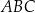 jest więc równe
jest więc równe
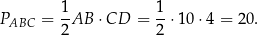
Sposób II
Jeżeli nie zauważyliśmy, że punkt 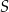 leży na prostej
leży na prostej 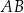 , to żaden dramat – zaczynamy od wyznaczenia współrzędnych punktów
, to żaden dramat – zaczynamy od wyznaczenia współrzędnych punktów 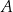 i
i 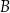 . Podstawiamy
. Podstawiamy
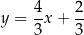
do równania okręgu.
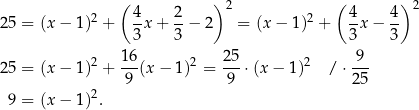
Stąd
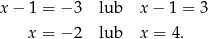
Stąd 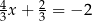 i
i 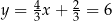 odpowiednio. To oznacza, że punkty
odpowiednio. To oznacza, że punkty 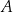 i
i 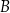 mają współrzędne
mają współrzędne  i
i 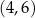 , przy czym nie wiemy, w jakiej kolejności. Zauważmy jednak, że wybór współrzędnych punktu
, przy czym nie wiemy, w jakiej kolejności. Zauważmy jednak, że wybór współrzędnych punktu 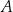 nie ma wpływu na wartość obliczonego pola trójkąta
nie ma wpływu na wartość obliczonego pola trójkąta 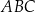 , bo obie sytuacje różnią się o symetrię osiową względem prostej prostopadłej do
, bo obie sytuacje różnią się o symetrię osiową względem prostej prostopadłej do 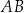 i przechodzącej przez punkt
i przechodzącej przez punkt  . Możemy więc bez zmniejszania ogólności założyć, że
. Możemy więc bez zmniejszania ogólności założyć, że 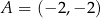 i
i 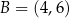 . Obliczmy długość odcinka
. Obliczmy długość odcinka 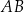 (ta długość jest nam potrzebna do obliczenia pola trójkąta
(ta długość jest nam potrzebna do obliczenia pola trójkąta 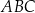 ).
).
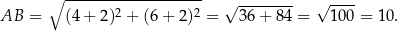
Ponieważ 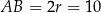 , po raz kolejny mamy okazję zauważyć, że
, po raz kolejny mamy okazję zauważyć, że 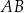 jest średnicą okręgu. Możemy wtedy tak samo jak w sposobie I obliczyć pole trójkąta
jest średnicą okręgu. Możemy wtedy tak samo jak w sposobie I obliczyć pole trójkąta 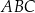 bez wyznaczania współrzędnych punktu
bez wyznaczania współrzędnych punktu 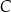 .
.
Przyjmijmy jednak, że nadal nie zauważyliśmy, że trójkąt 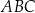 jest prostokątny. W takiej sytuacji – zmierzamy w kierunku wyznaczenia współrzędnych punktu
jest prostokątny. W takiej sytuacji – zmierzamy w kierunku wyznaczenia współrzędnych punktu 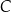 . Najpierw jednak wyznaczmy współrzędne punktu
. Najpierw jednak wyznaczmy współrzędne punktu 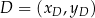 – najprościej to zrobić przy użyciu wektorów.
– najprościej to zrobić przy użyciu wektorów.
![−→ −→ AD = 4AB = 4[4+ 2,6+ 2] [5 ]5 24 3 2 [xD + 2,yD + 2] = 5-,-5- .](https://img.zadania.info/zad/5928397/HzadR50x.png)
Mamy stąd
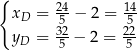
i 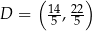 . Piszemy teraz równanie prostej
. Piszemy teraz równanie prostej 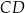 – jest ona prostopadła do prostej
– jest ona prostopadła do prostej 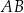 , więc ma równanie postaci
, więc ma równanie postaci
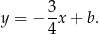
Współczynnik 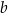 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 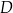 .
.
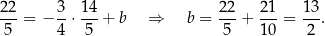
Prosta 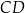 ma więc równanie
ma więc równanie 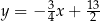 .
.
Szukamy teraz punktów wspólnych prostej 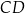 i danego okręgu (czyli wyznaczamy możliwe współrzędne punktu
i danego okręgu (czyli wyznaczamy możliwe współrzędne punktu  ). Podstawiamy
). Podstawiamy 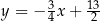 do równania okręgu.
do równania okręgu.

Rozwiązujemy otrzymane równanie kwadratowe
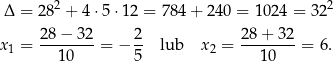
Mamy wtedy

Zatem 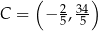 lub
lub 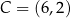 . Obliczamy teraz długość odcinka
. Obliczamy teraz długość odcinka 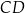 (czyli wysokości trójkąta
(czyli wysokości trójkąta  ) w każdym z tych przypadków.
) w każdym z tych przypadków.
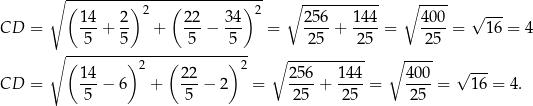
To oznacza, że w obu przypadkach pole trójkąta 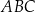 jest równe
jest równe
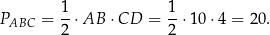
Odpowiedź: