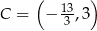Zadanie nr 1309148
Punkt 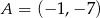 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 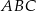 , w którym
, w którym 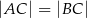 . Obie współrzędne wierzchołka
. Obie współrzędne wierzchołka 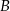 są liczbami dodatnimi. Okrąg wpisany w trójkąt
są liczbami dodatnimi. Okrąg wpisany w trójkąt 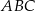 ma równanie
ma równanie 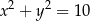 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 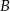 i
i 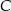 tego trójkąta.
tego trójkąta.
Rozwiązanie
Szkicujemy opisaną sytuację.
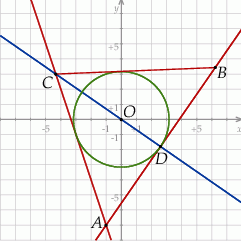
Rozpoczniemy od napisania równań stycznych do danego okręgu poprowadzonych z punktu 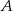 . Każda prosta, która nie jest pionowa i przechodzi przez punkt
. Każda prosta, która nie jest pionowa i przechodzi przez punkt 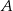 ma równanie postaci
ma równanie postaci
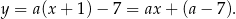
Są różne sposoby ustalenia dla jakich wartości  prosta tej postaci jest styczna do danego okręgu, można np. wstawić
prosta tej postaci jest styczna do danego okręgu, można np. wstawić 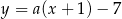 do równania okręgu i sprawdzić, kiedy otrzymane równanie ma dokładnie jedno rozwiązanie (licząc deltę). Inny sposób to skorzystać ze wzoru na odległość punktu
do równania okręgu i sprawdzić, kiedy otrzymane równanie ma dokładnie jedno rozwiązanie (licząc deltę). Inny sposób to skorzystać ze wzoru na odległość punktu 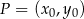 od prostej
od prostej 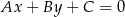 :
:
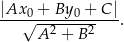
W naszej sytuacji odległość punktu  od prostej
od prostej 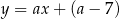 musi być równa
musi być równa 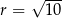 . Sprawdzamy kiedy tak jest.
. Sprawdzamy kiedy tak jest.
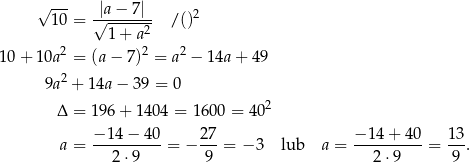
Proste 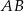 i
i 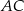 mają więc odpowiednio równania:
mają więc odpowiednio równania:
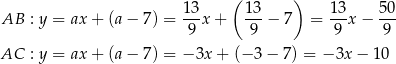
(w tym miejscu korzystamy z tego, że punkt 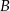 ma obie współrzędne dodatnie – dlatego drugie z równań nie może określać prostej
ma obie współrzędne dodatnie – dlatego drugie z równań nie może określać prostej 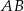 ). Zauważmy teraz, że łatwo jest napisać równanie osi symetrii
). Zauważmy teraz, że łatwo jest napisać równanie osi symetrii 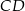 trójkąta
trójkąta 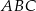 (czyli jego wysokości/dwusiecznej poprowadzonej z wierzchołka
(czyli jego wysokości/dwusiecznej poprowadzonej z wierzchołka 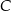 ). Jest to prosta prostopadła do podstawy
). Jest to prosta prostopadła do podstawy 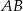 i przechodząca przez środek
i przechodząca przez środek 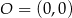 okręgu wpisanego. Jest to więc prosta
okręgu wpisanego. Jest to więc prosta 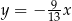 . Szukamy teraz jej punktu wspólnego
. Szukamy teraz jej punktu wspólnego 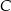 z prostą
z prostą 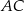 .
.
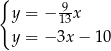
Odejmujemy od pierwszego równania drugie i mamy
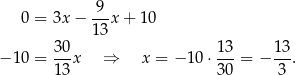
Stąd 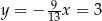 i
i 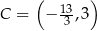 .
.
Wyznaczmy jeszcze punkt wspólny 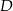 prostych
prostych 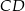 i
i 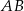 .
.
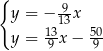
Odejmujemy od drugiego równania pierwsze i mamy
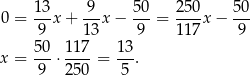
Stąd 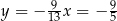 i
i 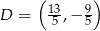 . Pozostało teraz obliczyć współrzędne punktu
. Pozostało teraz obliczyć współrzędne punktu  – korzystamy z tego, że punkt
– korzystamy z tego, że punkt  jest środkiem podstawy
jest środkiem podstawy  .
.
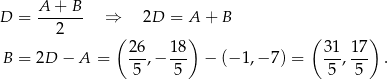
Odpowiedź: 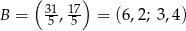 ,
,