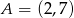/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Równoramienny

Zadanie nr 1858695

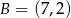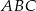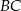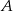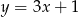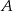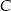Punkt B = (7,2) jest wierzchołkiem trójkąta równoramiennego ABC o podstawie BC . Pole tego trójkąta jest równe 20, a wysokość poprowadzona z wierzchołka A tego trójkąta zawiera się w prostej o równaniu y = 3x + 1 . Oblicz współrzędne punktów A i C . Rozważ wszystkie przypadki.

Wersja PDF

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

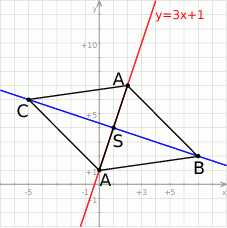
Na początku napiszmy równanie podstawy 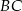BC – jest to prosta prostopadła do podanej wysokości, więc ma równanie postaci 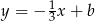y = − 13x + b . Współczynnik 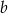b wyznaczamy podstawiając współrzędne punktu B .

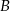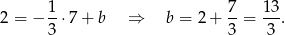
1- 7- 1-3 2 = − 3 ⋅7 + b ⇒ b = 2 + 3 = 3 .

Prosta 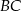BC ma więc równanie 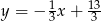y = − 1x + 13- 3 3 . Szukamy teraz jej punktu wspólnego 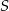S z podaną wysokością (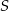S jest środkiem boku BC ).

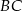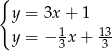
{ y = 3x + 1 1 13 y = − 3 x+ 3-

Odejmujemy od pierwszego równania drugie i mamy

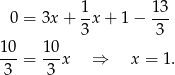
0 = 3x + 1-x+ 1− 13- 3 3 10 10 ---= ---x ⇒ x = 1 . 3 3

Stąd 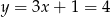y = 3x + 1 = 4 i S = (1 ,4 ) .

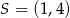Teraz łatwo wyznaczyć współrzędne punktu 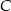C – korzystamy z tego, że punkt S jest środkiem odcinka BC .

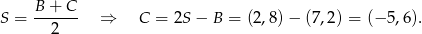
B + C S = ------ ⇒ C = 2S − B = (2,8)− (7,2) = (− 5,6). 2

Stąd

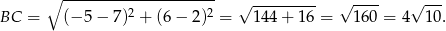
∘ --------------------- 2 2 √ --------- √ ---- √ --- BC = (− 5 − 7) + (6− 2) = 144 + 16 = 160 = 4 10.

Pora wykorzystać podaną informację o polu trójkąta 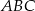ABC .

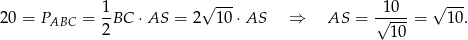
1 √ --- 10 √ --- 20 = PABC = -BC ⋅AS = 2 10⋅AS ⇒ AS = √----= 10. 2 10

Szukamy teraz punktu 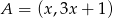A = (x ,3x + 1) na podanej wysokości 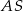AS , dla którego --- AS = √ 10 .

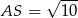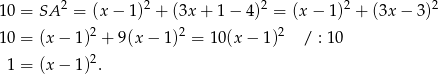
10 = SA 2 = (x− 1)2 + (3x + 1− 4)2 = (x − 1)2 + (3x − 3)2 2 2 2 10 = (x − 1 ) + 9(x − 1 ) = 10(x − 1) / : 10 1 = (x − 1 )2.

Stąd

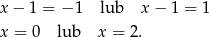
x− 1 = − 1 lub x − 1 = 1 x = 0 lub x = 2 .

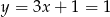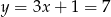Mamy wtedy y = 3x + 1 = 1 i y = 3x+ 1 = 7 odpowiednio. Zatem 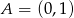A = (0,1) lub A = (2,7) .  
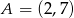Odpowiedź: 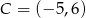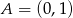C = (− 5,6) , A = (0,1 ) lub A = (2,7)

Wersja PDF