/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Równoramienny

Zadanie nr 3107632

Punkty 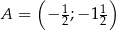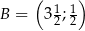( 1 1) A = − 2;− 12 , ( 1 1) B = 32 ;2 są wierzchołkami trójkąta równoramiennego 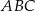ABC o podstawie 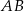AB . Ramię 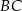BC zawiera się w prostej o równaniu 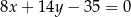8x + 14y − 35 = 0 . Oblicz współrzędne punktu 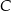C i pole tego trójkąta.

Wersja PDF

Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

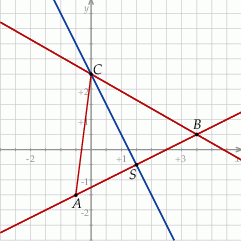
Środek 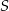S odcinka 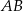AB ma współrzędne

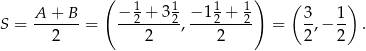
( 1 1 1 1 ) ( ) A--+-B- −-2-+-32- −-12-+-2- 3- 1- S = 2 = 2 , 2 = 2,− 2 .

Sposób I

Ponieważ trójkąt 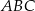ABC jest równoramienny i 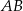AB jest jego podstawą, wierzchołek 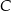C leży na symetralnej odcinka 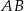AB . Napiszmy równanie tej symetralnej. Jest to zbiór punktów 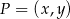P = (x ,y) , dla których

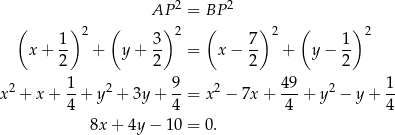
2 2 AP = BP ( 1) 2 ( 3) 2 ( 7) 2 ( 1) 2 x+ -- + y+ -- = x− -- + y− -- 2 2 2 2 2 1- 2 9- 2 4-9 2 1- x + x+ 4 + y + 3y + 4 = x − 7x + 4 + y − y+ 4 8x + 4y − 10 = 0.

Szukamy teraz punktu wspólnego 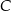C tej symetralnej z podaną prostą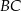 BC

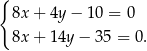
{ 8x + 4y− 10 = 0 8x + 14y− 35 = 0.

Odejmujemy od drugiego równania pierwsze i mamy

25- 5- 10y − 2 5 = 0 ⇐ ⇒ y = 10 = 2.

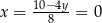Stąd x = 10−-4y= 0 8 i ( ) C = 0, 5 2 .

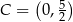Pozostało obliczyć pole trójkąta 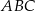ABC .

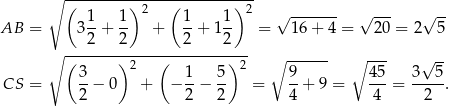
∘ -------------------------- ( ) 2 ( ) 2 √ ------- √ --- √ -- AB = 31-+ 1- + 1-+ 1 1- = 16 + 4 = 20 = 2 5 2 2 2 2 ∘ (------)-----(--------)--- ∘ ------ ∘ --- √ -- 3- 2 1- 5- 2 9- 45- 3--5- CS = 2 − 0 + − 2 − 2 = 4 + 9 = 4 = 2 .

Pole trójkąta 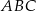ABC jest więc równe

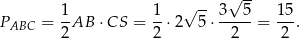
√ -- 1- 1- √ -- 3--5- 15- PABC = 2AB ⋅CS = 2 ⋅2 5⋅ 2 = 2 .

Sposób II

Wiemy, że punkt 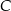C leży na prostej

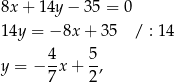
8x + 14y − 3 5 = 0 14y = − 8x+ 35 / : 14 4 5 y = − 7-x + 2-,

więc ma współrzędne postaci 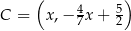( ) C = x ,− 4x+ 5 7 2 . Wiemy ponadto, że trójkąt 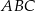ABC jest równoramienny, więc

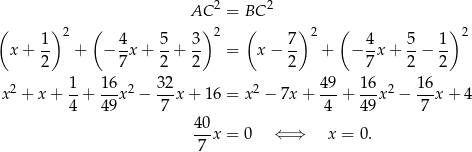
2 2 AC = BC ( 1 )2 ( 4 5 3) 2 ( 7 )2 ( 4 5 1) 2 x + -- + − -x + -+ -- = x − -- + − -x + --− -- 2 7 2 2 2 7 2 2 2 1- 1-6 2 32- 2 49- 16- 2 16- x + x+ 4 + 4 9x − 7 x+ 16 = x − 7x + 4 + 49 x − 7 x+ 4 40 ---x = 0 ⇐ ⇒ x = 0. 7

Stąd 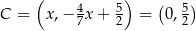( ) ( ) C = x,− 47 x+ 52 = 0, 52 .

Pole obliczamy tak samo jak w poprzednim sposobie.  
Odpowiedź: 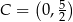( 5 ) C = 0,2 , 15 PABC = 2

Wersja PDF