Zadanie nr 3700173
W równoramiennym trójkącie prostokątnym punkt 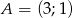 jest wierzchołkiem kąta ostrego. Przeciwległa do niego przyprostokątna zawiera się w prostej o równaniu
jest wierzchołkiem kąta ostrego. Przeciwległa do niego przyprostokątna zawiera się w prostej o równaniu 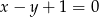 . Napisz równania prostych zawierających pozostałe boki trójkąta.
. Napisz równania prostych zawierających pozostałe boki trójkąta.
Rozwiązanie
Zaczynamy od rysunku.
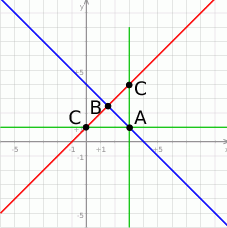
Łatwo jest napisać równanie boku 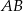 – jest to prosta prostopadła do podanej prostej i przechodząca przez punkt
– jest to prosta prostopadła do podanej prostej i przechodząca przez punkt 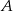 . Ma więc ona postać
. Ma więc ona postać 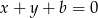 . Współczynnik
. Współczynnik 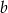 wyliczamy z faktu, że przechodzi ona przez
wyliczamy z faktu, że przechodzi ona przez 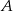

Zatem prosta 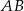 to
to 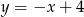 . Aby wyznaczyć trzeci wierzchołek, musimy znaleźć na prostej
. Aby wyznaczyć trzeci wierzchołek, musimy znaleźć na prostej 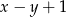 punkt
punkt 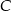 , taki, że
, taki, że 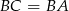 (bo trójkąt ma być równoramienny).
(bo trójkąt ma być równoramienny).
Wyliczmy najpierw punkt 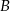 . W tym celu przecinamy proste
. W tym celu przecinamy proste 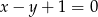 i
i 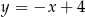 (od razu podstawiamy za
(od razu podstawiamy za 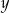 ).
).
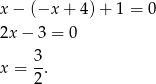
Zatem 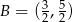 . Policzmy
. Policzmy 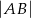 .
.
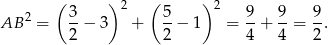
Szukamy teraz na prostej 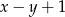 punktów, których kwadrat odległości od punktu
punktów, których kwadrat odległości od punktu 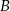 wynosi
wynosi 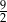 .
.
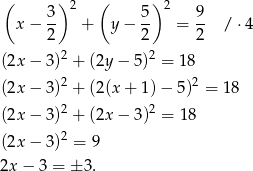
Stąd 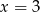 lub
lub 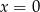 . Wtedy równanie boku
. Wtedy równanie boku 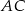 to
to 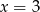 lub
lub 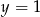 odpowiednio.
odpowiednio.
Wyznaczenie boku 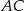 można było bardzo skrócić, jeżeli byśmy zauważyli, że musi on być poziomy lub pionowy. To ostatnie stwierdzenie wynika z faktu, że kąty ostre trójkąta
można było bardzo skrócić, jeżeli byśmy zauważyli, że musi on być poziomy lub pionowy. To ostatnie stwierdzenie wynika z faktu, że kąty ostre trójkąta 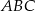 muszą wynosić
muszą wynosić 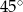 (bo jest równoramienny) oraz podana przyprostokątna tworzy dokładnie taki kąt z osią
(bo jest równoramienny) oraz podana przyprostokątna tworzy dokładnie taki kąt z osią 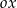 . Druga z nich musi więc z tą osią tworzyć kąt
. Druga z nich musi więc z tą osią tworzyć kąt 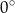 lub
lub 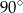 .
.
Odpowiedź: 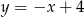 ,
, 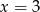 lub
lub 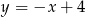 ,
,