Zadanie nr 4064606
Dany jest trójkąt równoramienny 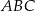 , w którym
, w którym 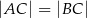 oraz
oraz 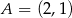 i
i 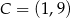 . Podstawa
. Podstawa 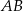 tego trójkąta jest zawarta w prostej
tego trójkąta jest zawarta w prostej 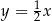 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 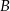 .
.
Rozwiązanie
Ponieważ punkt 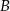 leży na prostej
leży na prostej 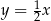 , więc ma on postać
, więc ma on postać 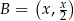 .
.
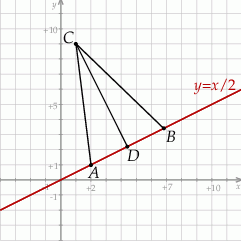
Zapiszmy teraz warunek 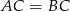 .
.
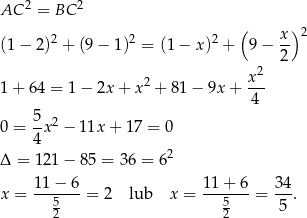
Pierwsze rozwiązanie daje współrzędne punktu 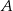 , więc musi być
, więc musi być 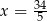 , czyli
, czyli 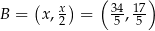 .
.
Sposób II
Napiszmy najpierw równanie wysokości 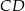 trójkąta
trójkąta 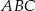 jest prosta postaci
jest prosta postaci 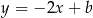 (bo jest prostopadła do
(bo jest prostopadła do 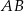 ) oraz przechodzi przez punkt
) oraz przechodzi przez punkt 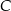 , więc
, więc

Szukamy teraz punktu wspólnego 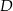 prostych
prostych 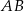 i
i 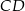 .
.
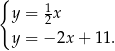
Odejmujemy od pierwszego równania drugie i mamy
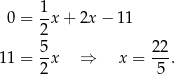
Stąd 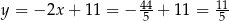 i
i 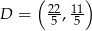 . Ponieważ trójkąt
. Ponieważ trójkąt 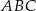 jest równoramienny, spodek wysokości
jest równoramienny, spodek wysokości 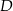 jest środkiem jego podstawy
jest środkiem jego podstawy 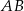 . Stąd
. Stąd
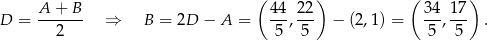
Odpowiedź: