/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Równoramienny

Zadanie nr 4177261

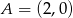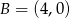W układzie współrzędnych na płaszczyźnie zaznaczono punkty A = (2 ,0) i B = (4,0) . Wyznacz wszystkie możliwe położenia punktu 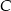C , dla których 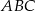ABC jest trójkątem równoramiennym o podstawie 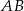AB i polu równym 3.

Wersja PDF

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

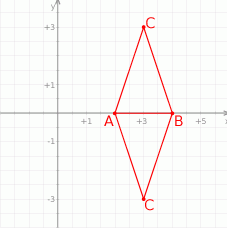
Z obrazka widać, że będą dwa takie punkty 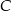C – położone symetrycznie względem osi 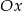Ox . Podstawa trójkąta 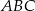ABC ma długość 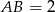AB = 2 , więc z podanej informacji o polu, możemy wyliczyć długość odpowiadającej wysokości.

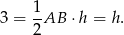
1 3 = -AB ⋅h = h. 2

Z drugiej strony, wysokość ta to po prostu odległość punktu 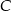C od osi 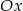Ox , czyli druga współrzędna punktu 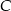C musi być równa 3 lub -3.

Pozostaje zauważyć, że punkt 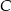C musi leżeć na symetralnej odcinka 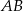AB (bo trójkąt ma być równoramienny), czyli na prostej 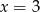x = 3 . Zatem 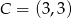C = (3,3) lub C = (3,− 3) .  
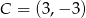Odpowiedź: 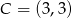C = (3,3) lub C = (3 ,−3 )

Wersja PDF