/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Równoramienny

Zadanie nr 4516139

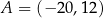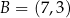Punkty A = (− 20,12 ) i B = (7,3) są wierzchołkami trójkąta równoramiennego 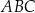ABC , w którym 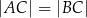|AC | = |BC | . Wierzchołek 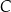C leży na osi 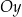Oy układu współrzędnych. Oblicz współrzędne wierzchołka 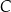C oraz obwód tego trójkąta.

Wersja PDF

Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

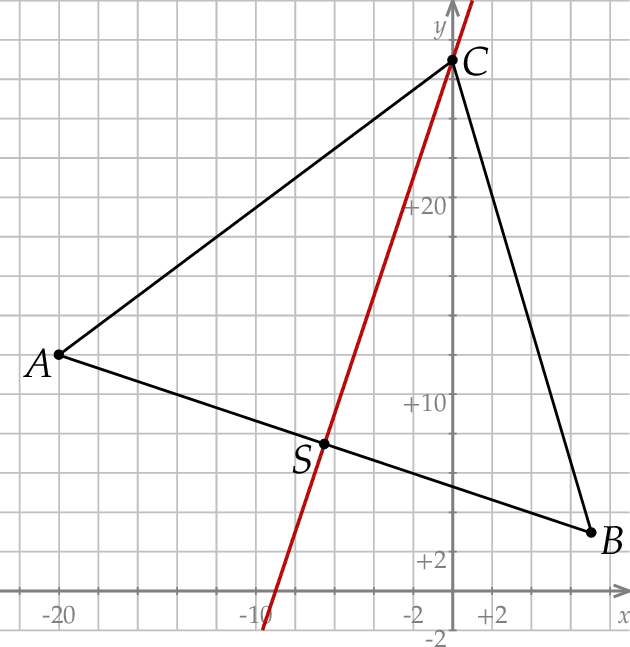
Sposób I

Szukamy punktu 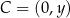C = (0,y) na podanej prostej, który spełnia równość: |AC | = |BC | .

|AC | = |BC | |AC |2 = |BC |2 2 2 2 2 (0 + 20 ) + (y − 12 ) = (0− 7) + (y − 3 ) 4 00+ y2 − 24y+ 144 = 4 9+ y2 − 6y + 9 4 86 = 18y ⇒ y = 27.

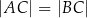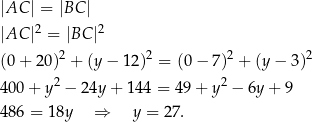
Zatem 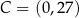C = (0,27) . To pozwala obliczyć długości boków trójkąta ABC .

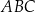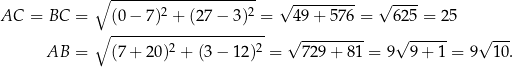
∘ -------------------- √ --------- √ ---- AC = BC = (0− 7)2 + (27− 3)2 = 49 + 576 = 625 = 25 ∘ ---------------------- --------- ------ --- AB = (7+ 20)2 + (3− 12)2 = √ 729 + 81 = 9√ 9 + 1 = 9√ 1 0.

Obwód trójkąta 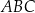ABC jest więc równy

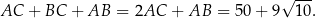
√ --- AC + BC + AB = 2AC + AB = 50+ 9 10.

Sposób II

Ponieważ trójkąt 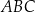ABC jest równoramienny i 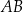AB jest jego podstawą, wierzchołek 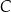C leży na symetralnej odcinka 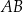AB . Napiszmy równanie tej symetralnej. Można to zrobić na wiele sposobów, my skorzystamy ze wzoru na równanie prostej przechodzącej przez punkt 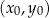(x0,y0) i prostopadłej do wektora →v = [p,q] .

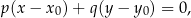
p(x − x0) + q(y − y0) = 0 ,

W naszej sytuacji mamy → −→ v = AB = [27,− 9] oraz

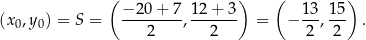
( −2 0+ 7 12 + 3 ) ( 1 3 15 ) (x0,y0) = S = --------,------- = − ---,--- . 2 2 2 2

Zatem symetralna odcinka 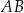AB ma równanie

( ) ( ) 27 x + 1-3 − 9 y− 15- = 0 / : 9 2 2 39 15 3x + ---− y + ---= 0 2 2 3x − y + 27 = 0.

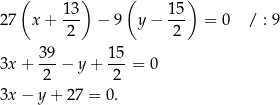
Pozostało teraz znaleźć punkt wspólny tej prostej z prostą 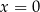x = 0 . Podstawiamy w powyższym równaniu x = 0 .

−y + 27 = 0 ⇒ y = 27.

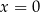Zatem 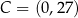C = (0,27) . Obwód trójkąta 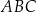ABC obliczamy tak samo jak w poprzednim sposobie.  
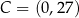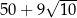Odpowiedź: C = (0,27) , obwód: √ --- 50+ 9 10 .

Wersja PDF