Zadanie nr 4946161
Odcinek 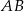 , gdzie
, gdzie 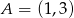 i
i 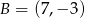 , jest podstawą trójkąta
, jest podstawą trójkąta 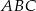 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 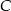 tak, aby trójkąt
tak, aby trójkąt 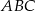 był równoramienny, a jego pole było równe 30.
był równoramienny, a jego pole było równe 30.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
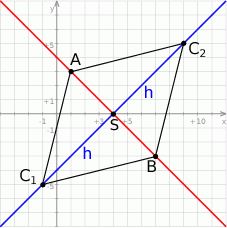
Obliczmy długość podstawy 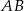 :
:
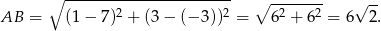
Z podanego pola mamy zatem
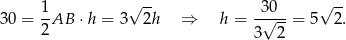
gdzie 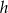 jest wysokością opuszczoną na bok
jest wysokością opuszczoną na bok 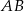 .
.
Sposób I
Jeden z możliwych sposobów wyznaczenia punktu 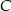 , to znalezienie punktów wspólnych okręgów o środkach w punktach
, to znalezienie punktów wspólnych okręgów o środkach w punktach 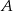 i
i 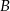 i promieniu
i promieniu
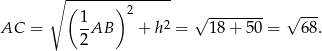
Musimy zatem rozwiązać układ równań.
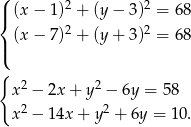
Odejmujemy teraz od pierwszego równania drugie (żeby skrócić kwadraty) i mamy

Podstawiamy tę wartość do pierwszego z równań
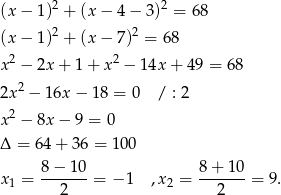
Stąd odpowiednio
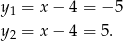
Zatem
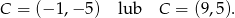
Sposób II
Trójkąt 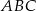 ma być równoramienny zatem wierzchołek
ma być równoramienny zatem wierzchołek 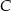 musi leżeć na symetralnej odcinka
musi leżeć na symetralnej odcinka 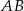 . Wyznaczamy środek odcinka
. Wyznaczamy środek odcinka 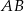 .
.
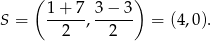
Wyznaczamy równanie prostej przechodzącej przez punkty 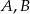 . Szukamy prostej w postaci
. Szukamy prostej w postaci 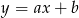 .
.
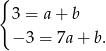
Odejmujemy stronami równania i otrzymujemy
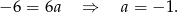
Zatem

Teraz wyznaczymy prostą prostopadłą do prostej przechodzącej przez punkty 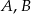 i przechodzącą przez punkt
i przechodzącą przez punkt 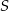 (czyli symetralną odcinka
(czyli symetralną odcinka 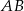 ). Musi ona mieć postać
). Musi ona mieć postać 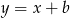 . Podstawiając współrzędne punktu
. Podstawiając współrzędne punktu 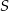 obliczamy
obliczamy 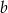 .
.

Zatem symetralna ma równanie 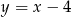 .
.
Ponieważ wierzchołek 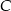 leży na symetralnej w odległości
leży na symetralnej w odległości 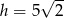 od punktu
od punktu 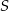 , więc leży na okręgu o środku w punkcie
, więc leży na okręgu o środku w punkcie 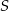 i promieniu
i promieniu 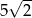 . Zapiszmy równanie tego okręgu
. Zapiszmy równanie tego okręgu

Otrzymujemy zatem układ równań
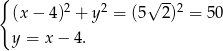
Podstawiamy drugie równanie do pierwszego i liczymy
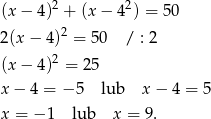
Zatem
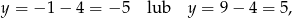
czyli
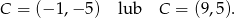
Sposób III
Postępujemy podobnie jak w poprzednim sposobie, wyliczamy najpierw współrzędne środka 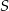 odcinka
odcinka 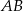 :
:
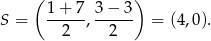
Teraz napiszemy równanie prostej zawierającej wysokość  . Korzystamy ze wzoru na równanie prostej prostopadłej do wektora
. Korzystamy ze wzoru na równanie prostej prostopadłej do wektora ![→v = [p,q]](https://img.zadania.info/zad/4946161/HzadR47x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 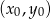
W naszej sytuacji ![→ → v = AB = [6,− 6]](https://img.zadania.info/zad/4946161/HzadR50x.gif) i
i 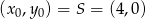 . Zatem równanie wysokości ma postać
. Zatem równanie wysokości ma postać
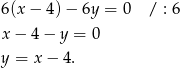
Pozostało znaleźć na tej prostej punkty 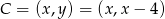 , dla których
, dla których 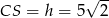 . Daje to nam równanie
. Daje to nam równanie
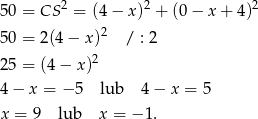
Tak jak w poprzednich sposobach otrzymujemy stąd
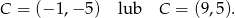
Odpowiedź: 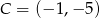 lub
lub