Zadanie nr 5553102
Podstawa trójkąta równoramiennego zawiera się w prostej 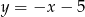 , a jedno z jego ramion w prostej
, a jedno z jego ramion w prostej 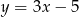 . Wyznacz równanie drugiego ramienia tego trójkąta, jeżeli jednym z jego wierzchołków jest punkt o współrzędnych
. Wyznacz równanie drugiego ramienia tego trójkąta, jeżeli jednym z jego wierzchołków jest punkt o współrzędnych 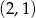 .
.
Rozwiązanie
Możemy zacząć od szkicowego rysunku.
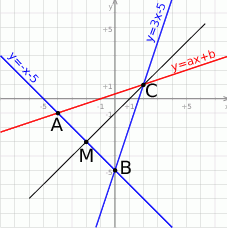
Wyliczmy współrzędne punktu 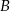 .
.
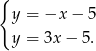
Odejmujemy od drugiego równania pierwsze (żeby skrócić 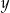 ) i mamy
) i mamy
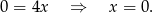
Stąd 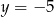 . Zatem
. Zatem 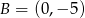 .
.
Sposób I
Powiedzmy, że szukamy prostej 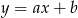 . Wyliczymy współrzędne punktu
. Wyliczymy współrzędne punktu 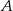 i sprawdzimy kiedy
i sprawdzimy kiedy 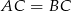 .
.
Zacznijmy od zauważenia, że jeżeli punkt 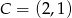 leży na szukanej prostej
leży na szukanej prostej 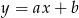 to
to
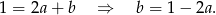
Teraz wyliczmy współrzędne punktu 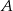
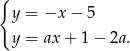
Jak poprzednio, odejmujemy od drugiego równania pierwsze i mamy
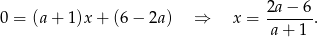
Powinniśmy jeszcze popatrzeć, co się dzieje jak 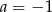 . Wtedy jednak proste
. Wtedy jednak proste 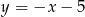 i
i 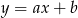 są równoległe i nie mają punktu przecięcia. Wyliczmy jeszcze
są równoległe i nie mają punktu przecięcia. Wyliczmy jeszcze 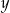 .
.
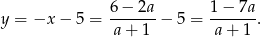
Zatem 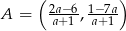 .
.
Pozostało sprawdzić kiedy 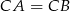 (od razu porównujemy kwadraty odległości).
(od razu porównujemy kwadraty odległości).
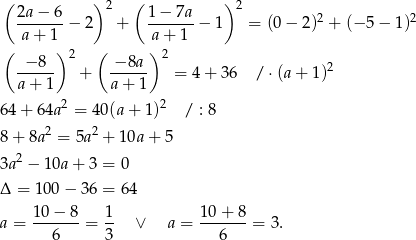
Drugie rozwiązanie daje nam prostą 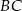 , więc wybieramy
, więc wybieramy 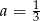 . Wtedy
. Wtedy
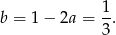
Sposób II
Tym razem zamiast bawić się w parametry spróbujmy lepiej wykorzystać to, co mamy.
Łatwo możemy napisać równanie symetralnej odcinka 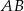 : jest to prosta prostopadła do
: jest to prosta prostopadła do 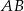 , czyli postaci
, czyli postaci 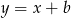 i przechodzi przez
i przechodzi przez 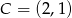 . Z tego drugiego warunku wyliczamy
. Z tego drugiego warunku wyliczamy 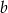 .
.
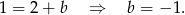
Zatem symetralna ma równanie 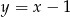 . Teraz szukamy jej punktu wspólnego
. Teraz szukamy jej punktu wspólnego 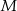 z prostą
z prostą 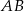 .
.
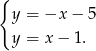
Dodając równania stronami mamy
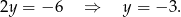
Stąd 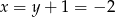 . Zatem
. Zatem 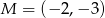 . No i fajnie, bo ten punkt to środek odcinka
. No i fajnie, bo ten punkt to środek odcinka 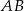 (bo trójkąt jest równoramienny). Jeżeli oznaczymy
(bo trójkąt jest równoramienny). Jeżeli oznaczymy 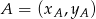 to ze wzoru na środek odcinka mamy
to ze wzoru na środek odcinka mamy
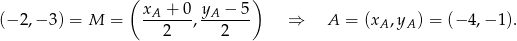
Pozostało teraz napisać równanie prostej 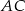 . Jeżeli szukamy prostej
. Jeżeli szukamy prostej 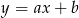 to mamy układ równań
to mamy układ równań
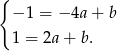
Odejmując od drugiego równania pierwsze mamy
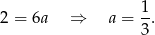
Zatem 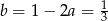 .
.
Sposób III
Zauważmy, że punkt 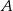 leży na danej prostej
leży na danej prostej 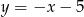 oraz na okręgu o środku
oraz na okręgu o środku 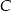 i promieniu
i promieniu
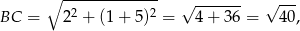
czyli na okręgu
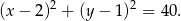
Szukamy punktów wspólnych tego okręgu z prostą 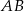 – podstawiamy
– podstawiamy 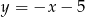 do równania okręgu.
do równania okręgu.
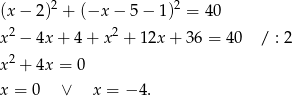
Pierwsze rozwiązanie prowadzi do punktu 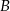 , więc mamy
, więc mamy 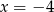 i
i 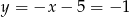 . Stąd
. Stąd 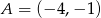 .
.
Teraz pozostało napisać równanie prostej 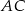 . Szukamy prostej w postaci
. Szukamy prostej w postaci 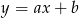 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 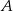 i
i 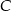 .
.
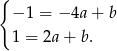
Odejmując od drugiego równania pierwsze mamy
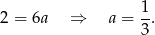
Zatem 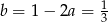 .
.
Odpowiedź: