Zadanie nr 5778467
Podstawa 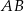 trójkąta równoramiennego
trójkąta równoramiennego 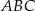 zawarta jest w prostej
zawarta jest w prostej 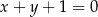 . Ramię
. Ramię 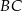 zawiera się w prostej
zawiera się w prostej 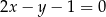 . Wyznacz równanie prostej
. Wyznacz równanie prostej 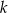 , zawierającej ramię
, zawierającej ramię 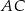 , wiedząc że punkt
, wiedząc że punkt 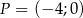 należy do prostej
należy do prostej 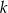 .
.
Rozwiązanie
Sposób I
Narysujmy najpierw szkicowy rysunek.
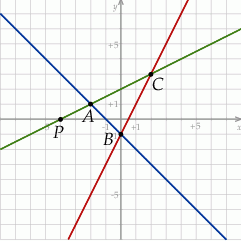
Od ręki możemy przeciąć podane proste i wyznaczyć współrzędne punktu 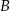 (prównujemy
(prównujemy 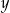 -ki).
-ki).
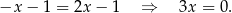
Stąd 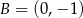 .
.
Plan jest następujący. Wybierzemy na prostej 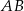 dowolny punkt
dowolny punkt 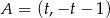 . Napiszemy równanie prostej
. Napiszemy równanie prostej 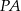 i znajdziemy jej punkt wspólny
i znajdziemy jej punkt wspólny 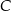 z prostą
z prostą 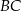 . Na koniec z warunku
. Na koniec z warunku 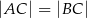 wyliczymy
wyliczymy 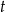 .
.
Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty 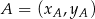 i
i 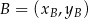 :
:
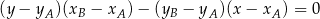
Korzystając z tego wzoru mamy równanie prostej 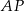
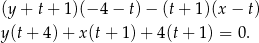
Szukamy teraz punktu przecięcia się tej prostej z prostą 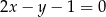 . Od razu podstawiamy za
. Od razu podstawiamy za 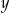 .
.
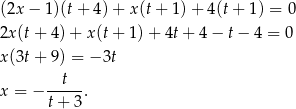
Stąd 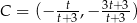 . Pozostało zapisać warunek
. Pozostało zapisać warunek 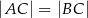 i rozwiązać odpowiednie równanie (od razu porównujemy kwadraty odległości).
i rozwiązać odpowiednie równanie (od razu porównujemy kwadraty odległości).
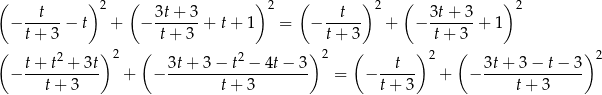
Mnożymy tę równość stronami przez 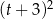 i mamy
i mamy
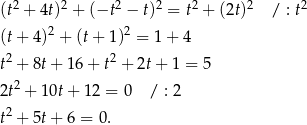
Dalej 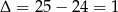 ,
, 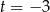 lub
lub 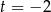 . Pierwsze z rozwiązań odrzucamy, gdyż wtedy proste
. Pierwsze z rozwiązań odrzucamy, gdyż wtedy proste 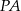 i
i 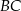 są równoległe. Zatem
są równoległe. Zatem 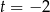 i prosta
i prosta 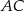 ma równanie
ma równanie
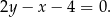
Sposób II
Tym razem wykorzystamy odrobinę więcej geometrii.
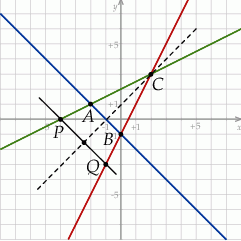
Zauważmy, że jeżeli poprowadzimy przez punkt 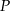 prostą równoległą do
prostą równoległą do 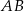 i znajdziemy jej punkt
i znajdziemy jej punkt 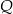 przecięcia się z prostą
przecięcia się z prostą 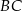 , to trójkąt
, to trójkąt 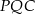 będzie również równoramienny. Będziemy więc w podobnej sytuacji jak na początku, ale tym razem będziemy znali oba wierzchołki podstawy. W takiej sytuacji wyznaczenie wierzchołka
będzie również równoramienny. Będziemy więc w podobnej sytuacji jak na początku, ale tym razem będziemy znali oba wierzchołki podstawy. W takiej sytuacji wyznaczenie wierzchołka 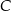 będzie już proste – napiszemy równanie symetralnej odcinka
będzie już proste – napiszemy równanie symetralnej odcinka 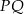 i przetniemy ją z prostą
i przetniemy ją z prostą 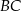 .
.
Liczymy, prosta 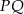 ma postać
ma postać 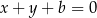 , wyliczamy
, wyliczamy 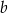
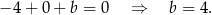
Szukamy punktu 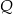 , czyli przecinamy proste
, czyli przecinamy proste 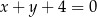 i
i 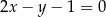 (od razu podstawiamy za
(od razu podstawiamy za  ).
).
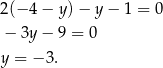
Zatem 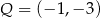 . Środek odcinka
. Środek odcinka 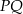 ma współrzędne
ma współrzędne 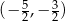 . Korzystamy teraz ze wzoru na równanie prostej prostopadłej do wektora
. Korzystamy teraz ze wzoru na równanie prostej prostopadłej do wektora ![→ v = [p,q]](https://img.zadania.info/zad/5778467/HzadR54x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 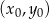
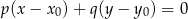
W naszej sytuacji ![→ −→ v = PQ = [3,− 3]](https://img.zadania.info/zad/5778467/HzadR57x.gif) . Stąd równanie symetralnej odcinka
. Stąd równanie symetralnej odcinka 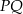 to
to
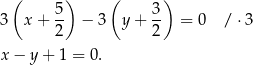
Szukamy punktu 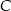 , czyli punktu wpólnego tej prostej z prostą
, czyli punktu wpólnego tej prostej z prostą 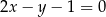 (porównujemy
(porównujemy 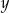 -ki).
-ki).
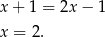
Stąd 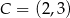 . Na zakończenie pozostało napisać równanie prostej
. Na zakończenie pozostało napisać równanie prostej 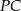 .
.
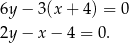
Odpowiedź: