/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Równoramienny

Zadanie nr 5974260

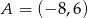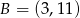Punkty A = (− 8,6) i B = (3,11) są wierzchołkami podstawy trójkąta równoramiennego 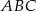ABC , a wysokość opuszczona z wierzchołka 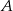A tego trójkąta zawiera się w prostej o równaniu 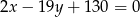2x − 19y + 130 = 0 . Oblicz współrzędne wierzchołka C .

Wersja PDF

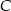Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

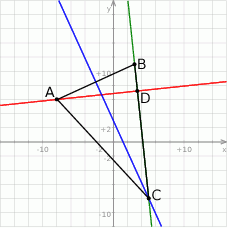
Napiszemy najpierw równanie prostej 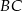BC – jest to prosta prostopadła do danej wysokości

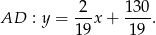
AD : y = 2-x + 1-30. 19 19

i przechodząca przez punkt 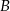B . Jest to więc prosta postaci 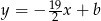y = − 192 x + b . Współczynnik 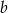b wyznaczamy podstawiając współrzędne punktu B .

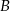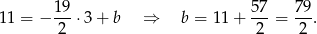
11 = − 19-⋅3 + b ⇒ b = 1 1+ 57-= 79. 2 2 2

Prosta 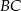BC ma więc równanie:

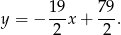
y = − 19-x+ 79-. 2 2

Wyznaczymy teraz równanie symetralnej odcinka 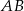AB . Można to zrobić na wiele różnych sposobów – my szukamy punktów 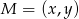M = (x,y ) , które są równo odległe od punktów 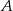A i B .

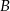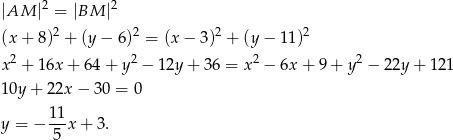
2 2 |AM | = |BM | (x + 8)2 + (y − 6)2 = (x − 3)2 + (y − 11)2 2 2 2 2 x + 16x + 64 + y − 1 2y+ 36 = x − 6x + 9 + y − 22y + 121 10y + 22x − 30 = 0 y = − 11x + 3. 5

Szukamy teraz punktu wspólnego 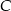C prostych: 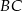BC i symetralnej odcinka AB .

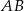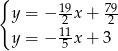
{ y = − 19x + 79 2 2 y = − 151x + 3

Odejmujemy od drugiego równania pierwsze (żeby skrócić 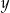y ) i mamy

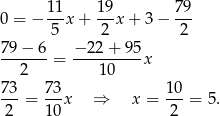
11- 19- 79- 0 = − 5 x + 2 x+ 3− 2 79 − 6 − 22 + 95 -------= ---------x 2 1 0 73-= 73-x ⇒ x = 10-= 5. 2 10 2

Stąd

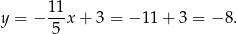
11 y = − ---x + 3 = − 11 + 3 = −8 . 5

i 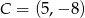C = (5,− 8) .  
Odpowiedź: C = (5,− 8)

Wersja PDF