/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Równoramienny

Zadanie nr 6018808

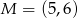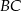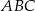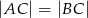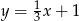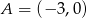Punkt M = (5 ,6) jest środkiem ramienia BC trójkąta równoramiennego ABC , w którym |AC | = |BC | . Podstawa AB tego trójkąta jest zawarta w prostej o równaniu y = 13x+ 1 oraz A = (−3 ,0) . Oblicz współrzędne wierzchołka 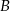B tego trójkąta.

Wersja PDF

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

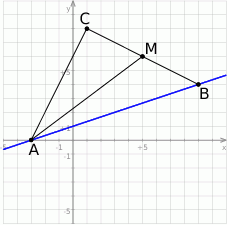
Wiemy, że wierzchołek 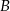B leży na prostej 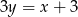3y = x + 3 , więc możemy jego współrzędne zapisać w postaci 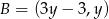B = (3y − 3,y) . Korzystamy teraz z informacji o tym, że 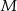M jest środkiem odcinka 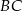BC i obliczamy współrzędne wierzchołka C .

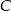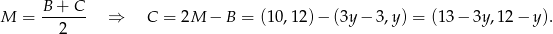
B + C M = ------ ⇒ C = 2M − B = (10 ,12)− (3y − 3,y) = (13− 3y ,12− y). 2

Pozostało teraz wykorzystać informację o tym, że

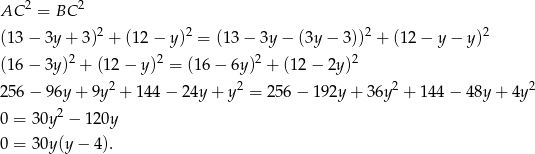
2 2 AC = BC (1 3− 3y + 3)2 + (1 2− y)2 = (13 − 3y − (3y − 3))2 + (12 − y − y)2 2 2 2 2 (1 6− 3y ) + (12− y) = (16 − 6y) + (12 − 2y) 2 2 2 2 2 56− 96y + 9y + 144 − 24y + y = 256 − 192y + 3 6y + 144 − 48y + 4y 0 = 30y2 − 120y 0 = 30y(y − 4).

Rozwiązanie 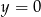y = 0 daje nam punkt 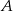A , więc je odrzucamy i mamy 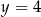y = 4 . Stąd

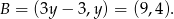
B = (3y− 3,y) = (9,4).

 
Odpowiedź: B = (9,4)

Wersja PDF