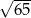Zadanie nr 6791411

Punkty 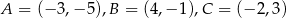A = (− 3,− 5),B = (4,− 1),C = (− 2,3) są wierzchołkami trójkąta równoramiennego. Oblicz długość ramienia tego trójkąta.

Wersja PDF

Rozwiązanie

Możemy spróbować naszkicować opisany w zadaniu trójkąt, ale przy odręcznym rysunku niespecjalnie widać, które dwa boki są równe.

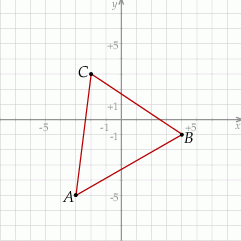
W takiej sytuacji obliczmy długości wszystkich trzech boków trójkąta 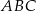ABC (żeby zobaczyć, które dwa są równe).

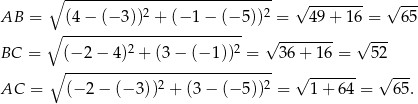
∘ ----------------------------- √ -------- √ --- AB = (4 − (− 3))2 + (− 1− (− 5))2 = 49 + 16 = 6 5 ∘ ------------------------- 2 2 √ -------- √ --- BC = ∘ (−-2−--4)-+--(3−--(−-1-))-=--- 36+ 16 = 52 2 2 √ ------- √ --- AC = (− 2 − (− 3)) + (3− (− 5)) = 1+ 64 = 65 .

Zatem ramię ma długość 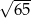√ --- 65 .
Odpowiedź: --- √ 65

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz