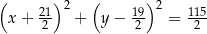Zadanie nr 7501233
Punkt  jest punktem przecięcia się środkowych trójkąta równoramiennego
jest punktem przecięcia się środkowych trójkąta równoramiennego  o podstawie
o podstawie  . Okrąg o średnicy
. Okrąg o średnicy 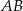 ma równanie
ma równanie 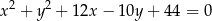 , a cięciwa tego okręgu równoległa do prostej
, a cięciwa tego okręgu równoległa do prostej 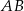 i przechodząca przez punkt
i przechodząca przez punkt 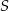 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 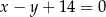 . Wyznacz równanie okręgu o środku
. Wyznacz równanie okręgu o środku 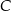 , który przechodzi przez punkty
, który przechodzi przez punkty 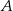 i
i 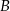 .
.
Rozwiązanie
Zacznijmy od przekształcenia równania okręgu tak, żeby widzieć jaki jest jego środek i promień.
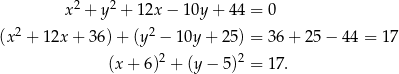
Jest to więc okrąg o środku 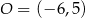 i promieniu
i promieniu 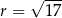 .
.
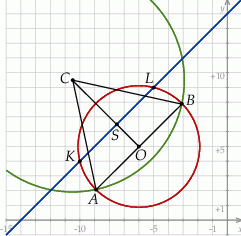
Znajdźmy teraz punkty wspólne tego okręgu z daną prostą – podstawiamy 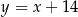 w równaniu okręgu.
w równaniu okręgu.
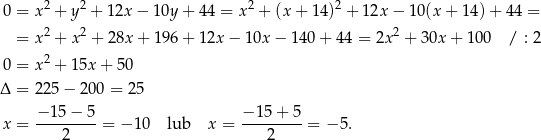
Stąd 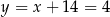 i
i 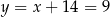 odpowiednio. Zatem
odpowiednio. Zatem 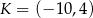 ,
, 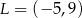 i
i
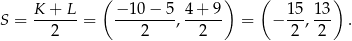
Chcielibyśmy teraz wyznaczyć współrzędne punktu 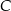 . Aby to zrobić musimy sięgnąć odrobinę głębiej do geometrii i przypomnieć sobie, że środek ciężkości trójkąta (punkt wspólny jego środkowych) dzieli każdą ze środkowych w stosunku 2:1 (licząc od wierzchołka). W takim razie
. Aby to zrobić musimy sięgnąć odrobinę głębiej do geometrii i przypomnieć sobie, że środek ciężkości trójkąta (punkt wspólny jego środkowych) dzieli każdą ze środkowych w stosunku 2:1 (licząc od wierzchołka). W takim razie 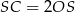 . Łatwo na tej podstawie wyznaczyć współrzędne punktu
. Łatwo na tej podstawie wyznaczyć współrzędne punktu  .
.
![−→ −→ SC = 2OS [ ] [ ] [ ] x + 15-,y− 13- = 2 − 15-+ 6, 1-3− 5 = 2 − 3-, 3 = [− 3,3 ]. 2 2 2 2 2 2](https://img.zadania.info/zad/7501233/HzadR14x.gif)
Stąd
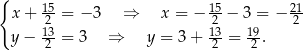
Zatem 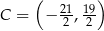 . Potrzebujemy jeszcze promień okręgu, czyli np. długość odcinka
. Potrzebujemy jeszcze promień okręgu, czyli np. długość odcinka 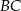 . Wiemy, że
. Wiemy, że 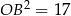 oraz
oraz
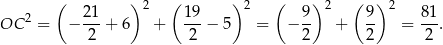
Stąd
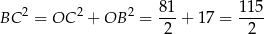
i szukany okrąg ma równanie
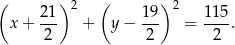
Odpowiedź: