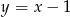Zadanie nr 7859655
Punkty 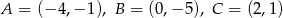 są wierzchołkami trójkąta równoramiennego. Wyznacz równanie osi symetrii tego trójkąta.
są wierzchołkami trójkąta równoramiennego. Wyznacz równanie osi symetrii tego trójkąta.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
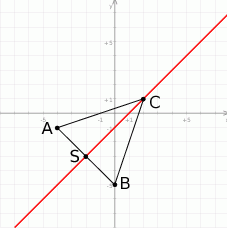
Z rysunku powinno być widać, że 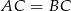 . Dla pewności sprawdźmy to.
. Dla pewności sprawdźmy to.
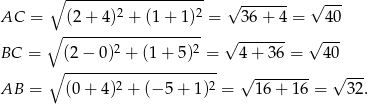
Policzyliśmy też długość 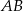 , żeby mieć pewność, że trójkąt nie jest równoboczny – wtedy miałby 3 osie symetrii.
, żeby mieć pewność, że trójkąt nie jest równoboczny – wtedy miałby 3 osie symetrii.
Szukana oś symetrii jest więc symetralną boku 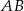 . Jak zwykle w geometrii analitycznej, możemy ją wyznaczyć na różne sposoby.
. Jak zwykle w geometrii analitycznej, możemy ją wyznaczyć na różne sposoby.
Sposób I
Szukana prosta jest prostą przechodzącą przez punkt 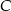 oraz przez środek
oraz przez środek
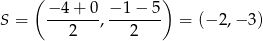
odcinka 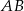 . Korzystamy teraz ze wzoru na równanie prostej przechodzącej przez dwa punkty
. Korzystamy teraz ze wzoru na równanie prostej przechodzącej przez dwa punkty 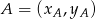 i
i 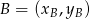 :
:
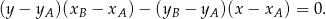
W naszym przypadku mamy (bierzemy 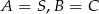 )
)
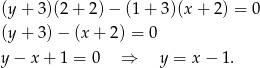
Sposób II
Szukana prosta jest prostopadła do 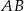 i przechodzi przez
i przechodzi przez 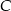 . W takiej sytuacji bardzo wygodny jest wzór na równanie prostej prostopadłej do wektora
. W takiej sytuacji bardzo wygodny jest wzór na równanie prostej prostopadłej do wektora ![→ v = [p,q]](https://img.zadania.info/zad/7859655/HzadR15x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 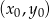
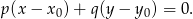
W naszej sytuacji mamy ![→ →v = AB = [4,− 4]](https://img.zadania.info/zad/7859655/HzadR18x.gif) , co daje równanie
, co daje równanie
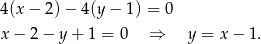
Sposób III
Możemy również myśleć o szukanej osi symetrii jak zbiorze punktów 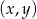 , które są równo odległe od punktów
, które są równo odległe od punktów 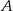 i
i 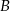 (symetralna odcinka
(symetralna odcinka 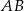 ). Daje to nam równość
). Daje to nam równość
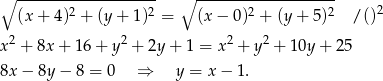
Odpowiedź: