Zadanie nr 8368390
Punkty 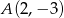 i
i 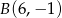 są końcami podstawy trójkąta równoramiennego
są końcami podstawy trójkąta równoramiennego 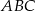 , którego pole jest równe 10. Wyznacz współrzędne wierzchołka
, którego pole jest równe 10. Wyznacz współrzędne wierzchołka  .
.
Rozwiązanie
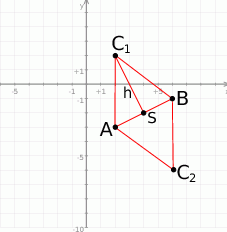
Zaczynamy od szkicowego rysunku.
Obliczmy długość podstawy 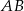 :
:
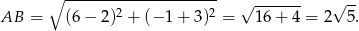
Z podanego pola mamy zatem
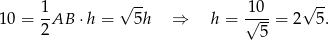
gdzie 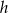 jest wysokością opuszczoną na bok
jest wysokością opuszczoną na bok 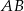 .
.
Sposób I
Jeden z możliwych sposobów wyznaczenia punktu 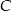 , to znalezienie punktów wspólnych okręgów o środkach w punktach
, to znalezienie punktów wspólnych okręgów o środkach w punktach 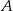 i
i 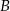 i promieniu
i promieniu
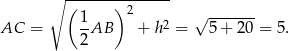
Musimy zatem rozwiązać układ równań.
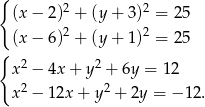
Odejmujemy teraz od pierwszego równania drugie (żeby skrócić kwadraty) i mamy
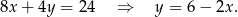
Podstawiamy tę wartość do pierwszego z równań
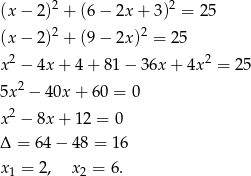
Stąd odpowiednio
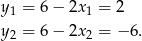
Sposób II
Tym razem zacznijmy od wyliczenia środka 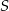 odcinka
odcinka 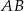 :
:
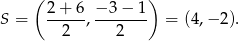
Teraz napiszemy równanie prostej zawierającej wysokość 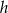 . Korzystamy ze wzoru na równanie prostej prostopadłej do wektora
. Korzystamy ze wzoru na równanie prostej prostopadłej do wektora ![→ v = [p,q]](https://img.zadania.info/zad/8368390/HzadR18x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 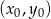
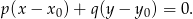
W naszej sytuacji ![→ →v = AB = [4,2]](https://img.zadania.info/zad/8368390/HzadR21x.gif) i
i 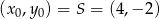 . Zatem równanie wysokości ma postać
. Zatem równanie wysokości ma postać
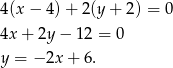
Pozostało znaleźć na tej prostej punkty 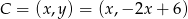 , dla których
, dla których 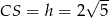 . Daje to nam równanie
. Daje to nam równanie
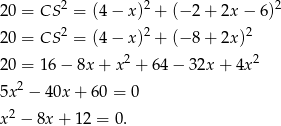
No i mamy to samo równanie co poprzednio.
Odpowiedź: 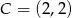 lub
lub