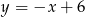Zadanie nr 8764949
W trójkącie równoramiennym  o podstawie
o podstawie  poprowadzono wysokość z wierzchołka
poprowadzono wysokość z wierzchołka  . Wyznacz równanie prostej zawierającej tę wysokość, jeśli
. Wyznacz równanie prostej zawierającej tę wysokość, jeśli 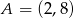 ,
, 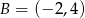 .
.
Rozwiązanie
Jeżeli naszkicujemy opisaną sytuację, to widać, że musimy napisać równanie symetralnej odcinka 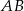 .
.
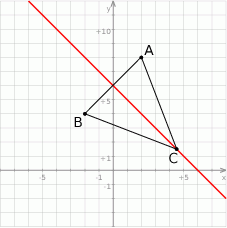
Sposób I
Możemy skorzystać ze wzoru na równanie prostej prostopadłej do wektora ![→ v = [p,q]](https://img.zadania.info/zad/8764949/HzadR2x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 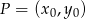
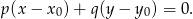
W naszej sytuacji mamy
![→v = A→B = [− 2 − 2,4 − 8] = [− 4,− 4]](https://img.zadania.info/zad/8764949/HzadR5x.gif)
oraz 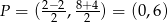 (środek odcinka
(środek odcinka 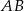 ). Zatem szukana prosta ma równanie
). Zatem szukana prosta ma równanie
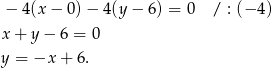
Sposób II
Jeżeli nie chcemy korzystać ze wzoru z wektorem, to piszemy najpierw równanie prostej 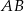 . Można skorzystać ze wzoru na równanie prostej przez dwa punkty, ale my obejdziemy się bez tego wzoru. Szukamy prostej postaci
. Można skorzystać ze wzoru na równanie prostej przez dwa punkty, ale my obejdziemy się bez tego wzoru. Szukamy prostej postaci 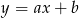 , na której leżą punkty o współrzędnych
, na której leżą punkty o współrzędnych 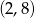 i
i 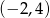 . Podstawiając te współrzędne do równania prostej otrzymujemy układ równań
. Podstawiając te współrzędne do równania prostej otrzymujemy układ równań
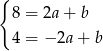
Odejmując od pierwszego równania drugie (żeby zredukować 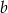 ) mamy
) mamy 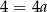 , czyli
, czyli 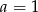 . Współczynnik
. Współczynnik 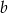 nie jest nam potrzebny, więc go nie wyliczamy.
nie jest nam potrzebny, więc go nie wyliczamy.
Symetralna odcinka 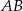 jest prostopadła do prostej
jest prostopadła do prostej 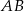 , więc jej współczynnik kierunkowy musi być równy
, więc jej współczynnik kierunkowy musi być równy 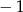 (bo pomnożony przez 1 ma dawać
(bo pomnożony przez 1 ma dawać 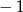 ). Zatem symetralna ta ma postać
). Zatem symetralna ta ma postać 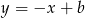 . Współczynnik
. Współczynnik 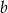 wyznaczamy podstawiając współrzędne środka odcinka
wyznaczamy podstawiając współrzędne środka odcinka 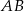 , czyli punktu
, czyli punktu 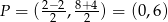 .
.
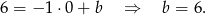
Zatem symetralna ma równanie 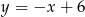 .
.
Sposób III
Symetralna to zbiór punktów 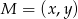 , które są równoodległe od obu końców odcinka. Punkty spełniają więc równanie
, które są równoodległe od obu końców odcinka. Punkty spełniają więc równanie
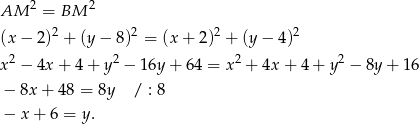
Odpowiedź: