/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Równoramienny

Zadanie nr 9922836

Dodaj do ulubionych
Dodaj do rozwiązanych

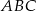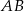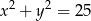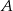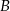Ostrokątny trójkąt równoramienny ABC o podstawie AB jest wpisany w okrąg o równaniu x2 + y2 = 25 . Punkty A i B leżą na prostej o równaniu y = x− 5 .

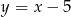  • Oblicz współrzędne punktów: A ,B,C .
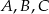  • Oblicz kąty trójkąta ABC .

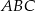Rozwiązanie

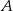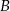  • Gdy naszkicujemy sobie opisaną sytuację jest jasne, że punkty A i B to punkty wspólne podanych prostej i okręgu.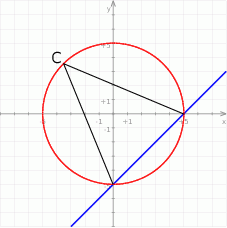
    PIC

    Zacznijmy od ich wyliczenia (wstawiamy 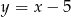y = x − 5 ) do równania okręgu.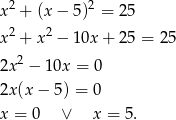

    x2 + (x − 5)2 = 25 2 2 x + x − 10x + 25 = 25 2x2 − 10x = 0 2x(x − 5) = 0 x = 0 ∨ x = 5.

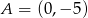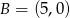    Zatem A = (0 ,−5 ) i B = (5,0) (lub na odwrót, ale nie ma to znaczenia). Aby wyznaczyć w ierzchołek 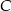C , musimy skorzystać z informacji, że trójkąt jest równoramienny. Wierzchołek 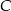C leży więc na symetralnej odcinka 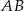AB – napiszemy teraz jej równanie. Najprościej jest skorzystać ze wzoru na równanie prostej prostopadłej do wektora → v = [p ,q] i przechodzącej przez punkt (x ,y ) 0 0

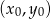
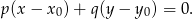
    p (x− x0)+ q(y− y0) = 0.

    W naszej sytuacji punkt to środek odcinka 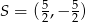S = ( 5,− 5) 2 2 , a wektor → → v = AB = [5,5] . Symetralna ma więc równanie

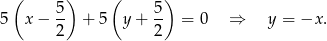
    ( ) ( ) 5 5 5 x − -- + 5 y + -- = 0 ⇒ y = −x . 2 2

    Szukamy teraz punktu wspólnego tej symetralnej z danym okręgiem.

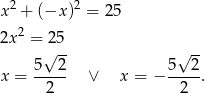
    x2 + (−x )2 = 25 2x2 = 25 √ -- √ -- x = 5--2- ∨ x = − 5---2. 2 2

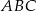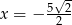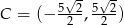    Aby ustalić, które z tych rozwiązań wybrać, musimy skorzystać z infomracji o tym, że trójkąt ABC jest ostrokątny. Z rysunku widać, że tak będzie tylko dla 5√ 2 x = − -2-- . Zatem 5√2 5√ 2 C = (− -2-, -2-) .  
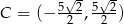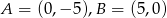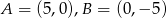
    Odpowiedź: √- √ - C = (− 5-2, 5-2) 2 2 , a A = (0,− 5),B = (5,0) lub A = (5,0 ),B = (0,− 5)

  • Ponieważ trójkąt jest równoramienny, wystarczy wyliczyć miarę kąta 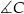∡C – pozostałe kąty są równe 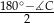∘ 180−2-∡C- . Miarę kąta 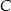C wyliczymy z twierdzenia sinusów, najpierw jednak policzmy długość boku AB .
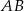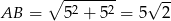
    ∘ -2----2 √ -- AB = 5 + 5 = 5 2

    Pozostało zastosować twierdzenie sinusów

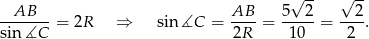
    √ -- √ -- AB AB 5 2 2 -------= 2R ⇒ sin∡C = ----= -----= ---. sin ∡C 2R 10 2

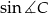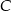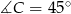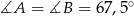    Teraz znowu musimy skorzystać z tego, że trójkąt jest równoramienny (inaczej sin ∡C nie wyznacza jednoznacznie kąta C ) i mamy ∡C = 45∘ . Zatem ∡A = ∡B = 67,5∘ .  
    Odpowiedź: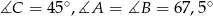 ∘ ∘ ∡C = 45 ,∡A = ∡B = 67,5 .

Wersja PDF