Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Zadanie nr 1207999

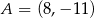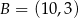Punkty A = (8,− 11) i B = (10,3) są końcami cięciwy okręgu o środku 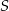S . Napisz równanie prostej prostopadłej do tej tej cięciwy i przechodzącej przez punkt S .

Wersja PDF
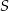Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

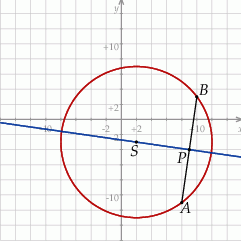
Nawet ze szkicowego rysunku powinno być jasne, że musimy napisać równanie symetralnej odcinka 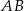AB .

Sposób I

Symetralna odcinka 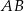AB to zbiór punktów 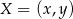X = (x,y) , które spełniają warunek

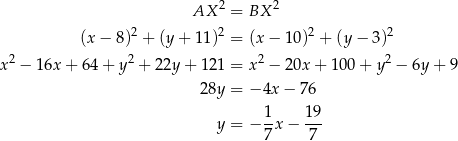
2 2 AX = BX 2 2 2 2 (x − 8 ) + (y + 11 ) = (x− 10) + (y− 3) x 2 − 1 6x+ 64 + y2 + 22y + 121 = x2 − 20x + 100 + y2 − 6y + 9 28y = − 4x− 76 1- 1-9 y = − 7x − 7

Sposób II

Prosta 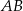AB ma współczynnik kierunkowy

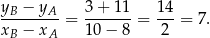
yB-−-yA- 3-+-11- 14- xB − x = 10 − 8 = 2 = 7. A

Zatem szukana prosta musi mieć równanie postaci 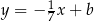1 y = − 7x + b . Przechodzi ona ponadto przez środek

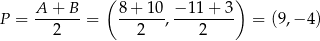
A + B ( 8 + 10 − 11+ 3) P = -------= -------,--------- = (9,− 4) 2 2 2

odcinka 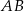AB . Mamy stąd

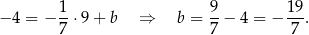
1 9 19 −4 = − --⋅9 + b ⇒ b = -− 4 = − ---. 7 7 7

 
Odpowiedź: 1 19 y = − 7x− 7-

Wersja PDF
Twoje uwagi
Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!