/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Różne

Zadanie nr 2023314

Dodaj do ulubionych
Dodaj do rozwiązanych

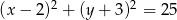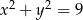Określ wzajemne położenie okręgów 2 2 (x − 2 ) + (y + 3) = 25 i 2 2 x + y = 9 .

Rozwiązanie

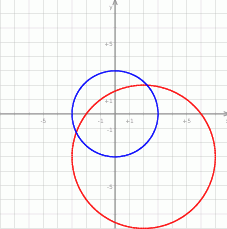
Możemy dokładnie narysować podane okręgi (cyrklem) i sprawdzić jakie jest ich wzajemne położenie. Czasami jednak trudno jest z rysunku ustalić dokładne położenie i dlatego skupimy się na metodach rachunkowych.

Sposób I

Najwygodniej jest skorzystać z następującej charakteryzacji wzajemnego położenia dwóch okręgów o środkach 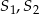S1,S2 i promieniach R 1 > R 2 .

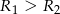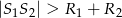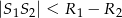  • Jeżeli |S 1S2| > R 1 + R 2 lub |S1S 2| < R 1 − R2 to okręgi są rozłączne (nie przecinają się)
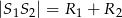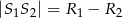  • Jeżeli |S1S2| = R 1 + R2 lub |S1S2| = R 1 − R2 to okręgi są styczne (przecinają się w jednym punkcie)
  • Jeżeli 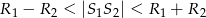R1 − R 2 < |S1S2| < R 1 + R 2 to okręgi przecinają się w dwóch punktach.

Jeżeli promienie okręgów są równe, to jest jeden dodatkowy wyjątek: jeżeli 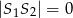|S1S 2| = 0 to okręgi pokrywają się.

Pierwszy okrąg ma środek 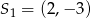S 1 = (2,− 3) i promień 5, drugi ma środek 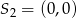S 2 = (0,0) i promień 3.

PIC

Mamy więc

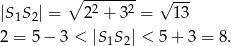
∘ ------- √ --- |S1S2| = 22 + 3 2 = 13 2 = 5 − 3 < |S S | < 5+ 3 = 8. 1 2

Zatem okręgi przecinają się w dwóch punktach.

Sposób II

Zadanie można też rozwiązać czysto algebraicznie.

Musimy sprawdzić ile rozwiązań ma układ równań

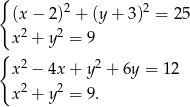
{ (x− 2)2 + (y+ 3)2 = 25 x2 + y2 = 9 { 2 2 x − 4x+ y + 6y = 12 x2 + y2 = 9.

Odejmujemy od pierwszego równania drugie (żeby skrócić kwadraty) i mamy

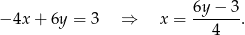
6y − 3 − 4x + 6y = 3 ⇒ x = ------. 4

Podstawimy teraz tę wartość do drugiego równania.

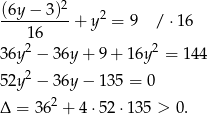
(6y-−-3)2- 2 1 6 + y = 9 / ⋅16 2 2 36y − 36y + 9 + 16y = 144 52y2 − 36y − 13 5 = 0 Δ = 3 62 + 4⋅52 ⋅135 > 0.

Skoro równanie ma dwa rozwiązania, to okręgi przecinają się w dwóch punktach.  
Odpowiedź: Okręgi przecinają się w dwóch punktach.

Wersja PDF