Zadanie nr 4315400
Okrąg o równaniu 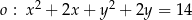 jest styczny do prostych
jest styczny do prostych 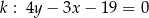 i
i 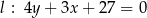 w punktach
w punktach 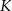 i
i 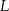 odpowiednio. Wyznacz równania wszystkich okręgów, które są jednocześnie styczne do okręgu
odpowiednio. Wyznacz równania wszystkich okręgów, które są jednocześnie styczne do okręgu  , prostych
, prostych 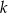 i
i 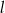 , oraz nie przechodzą przez punkty
, oraz nie przechodzą przez punkty 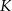 i
i 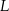 .
.
Rozwiązanie
Przekształćmy równanie danego okręgu tak, aby zobaczyć jaki ma promień i środek.
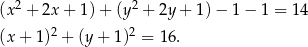
Jest to więc okrąg o środku 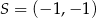 i promieniu
i promieniu 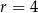 . Wyznaczmy jeszcze punkt wspólny
. Wyznaczmy jeszcze punkt wspólny 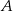 danych prostych
danych prostych
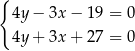
Dodajemy równania stronami i mamy 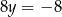 , czyli
, czyli 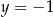 . Stąd
. Stąd
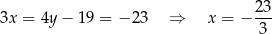
i 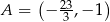 . Możemy teraz naszkicować opisaną sytuację.
. Możemy teraz naszkicować opisaną sytuację.
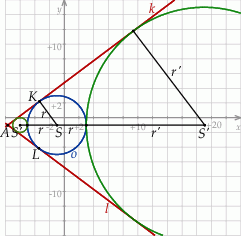
Widać, że będą dwa okręgi, które są jednocześnie styczne do 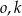 i
i 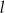 – jeden mniejszy, a drugi większy od danego okręgu (w tym miejscu korzystamy z założenia, że szukany okrąg nie przechodzi przez punkty
– jeden mniejszy, a drugi większy od danego okręgu (w tym miejscu korzystamy z założenia, że szukany okrąg nie przechodzi przez punkty 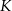 i
i 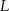 – bez tego założenia byłyby cztery okręgi spełniające warunki zadania). Widać też, że punkty
– bez tego założenia byłyby cztery okręgi spełniające warunki zadania). Widać też, że punkty 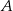 i
i 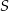 leżą na poziomej prostej
leżą na poziomej prostej 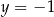 , która jest dwusieczną kąta utworzonego przez proste
, która jest dwusieczną kąta utworzonego przez proste 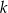 i
i 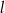 . Środki szukanych okręgów też leżą na tej prostej, więc mają współrzędne postaci
. Środki szukanych okręgów też leżą na tej prostej, więc mają współrzędne postaci 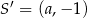 . Wartość współczynnika
. Wartość współczynnika  możemy obliczyć, porównując odległość punktu
możemy obliczyć, porównując odległość punktu 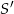 od okręgu
od okręgu  i jednej z prostych, powiedzmy
i jednej z prostych, powiedzmy 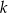 . Musimy zatem mieć
. Musimy zatem mieć
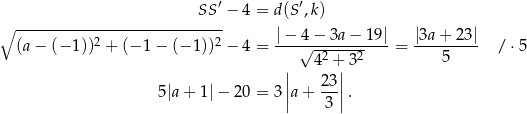
Rozwiązujemy teraz otrzymane równanie – rozważamy trzy przypadki.
Jeżeli 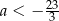 , to mamy równanie
, to mamy równanie
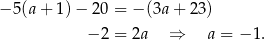
Liczba ta nie spełnia warunku: 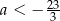 , więc równanie jest sprzeczne w tym przypadku.
, więc równanie jest sprzeczne w tym przypadku.
Jeżeli 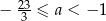 , to mamy równanie
, to mamy równanie
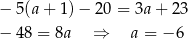
Ta liczba spełnia warunek: 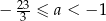 .
.
Jeżeli wreszcie 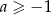 , to mamy równanie
, to mamy równanie
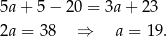
Ta liczba również jest rozwiązaniem interesującego nas równania. Mam więc 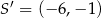 lub
lub 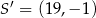 . Promień
. Promień 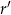 okręgu możemy w każdym z tych przypadków obliczyć z warunku
okręgu możemy w każdym z tych przypadków obliczyć z warunku
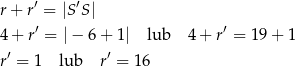
Są więc dwa okręgi spełniające warunki zadania:
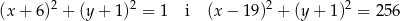
Odpowiedź: 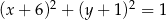 ,
,