/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Różne

Zadanie nr 4383161

Dodaj do ulubionych
Dodaj do rozwiązanych

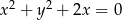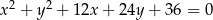Określ wzajemne położenie okręgów: 2 2 x + y + 2x = 0 i 2 2 x + y + 12x + 24y + 36 = 0 .

Rozwiązanie

Rozpoczynamy od zapisania równań okręgów tak, aby było widać jakie mają środki i promienie (zwijamy do pełnych kwadratów).

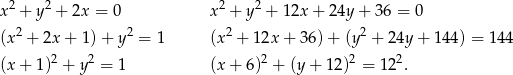
2 2 2 2 x + y + 2x = 0 x + y + 1 2x+ 24y + 36 = 0 (x2 + 2x + 1) + y2 = 1 (x 2 + 1 2x+ 36) + (y2 + 24y + 144 ) = 144 (x+ 1)2 + y2 = 1 (x + 6)2 + (y + 1 2)2 = 122.

Są to zatem odpowiednio: okrąg o środku 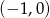(− 1,0) i promieniu 1, oraz okrąg o środku 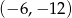(− 6,− 12) i promieniu 12.

Możemy teraz spróbować naszkicować opisaną sytuację – ponieważ jednak liczby są spore, trudno z rysunku mieć pewność czy okręgi przecinają się, czy też nie.

PIC

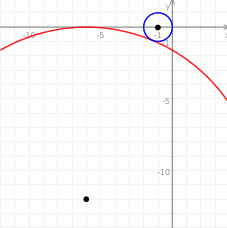
W takim układzie pozostają nam rachunki – sprawdźmy jaka jest odległość środków okręgów.

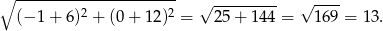
∘ ---------------------- √ --------- √ ---- (− 1+ 6)2 + (0+ 12)2 = 25 + 144 = 169 = 1 3.

Ponieważ jest to dokładnie suma promieni tych dwóch okręgów, muszą one być styczne.  
Odpowiedź: Okręgi są styczne zewnętrznie.

Wersja PDF