Zadanie nr 5692663
Punkt 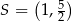 leży wewnątrz figury
leży wewnątrz figury 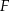 opisanej układem nierówności
opisanej układem nierówności
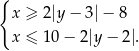
Wyznacz równanie największego okręgu o środku 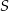 , który jest zawarty wewnątrz figury
, który jest zawarty wewnątrz figury 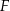 .
.
Rozwiązanie
Spróbujemy najpierw naszkicować zbiór 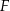 . Pierwszą z nierówności możemy zapisać w postaci
. Pierwszą z nierówności możemy zapisać w postaci
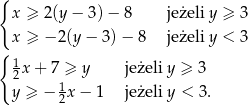
Analogicznie rozszyfrowujemy drugą nierówność
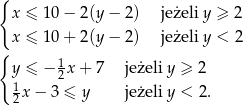
Dany w treści zadania układ nierówności możemy więc zapisać w postaci
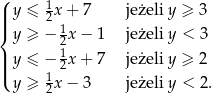
Szkicujemy teraz 4 pojawiające się w tym układzie nierówności proste:

i zaznaczmy zbiór 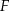 .
.
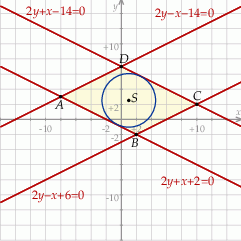
Gdy to zrobimy, okaże się, że jest to równoległobok 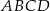 o wierzchołkach
o wierzchołkach 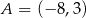 ,
, 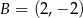 ,
, 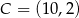 i
i 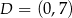 . Punkt
. Punkt 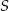 rzeczywiście znajduje się wewnątrz tego równoległoboku – obliczmy odległości tego punktu od boków równoległoboku (dzięki temu ustalimy jaki największy okrąg o środku
rzeczywiście znajduje się wewnątrz tego równoległoboku – obliczmy odległości tego punktu od boków równoległoboku (dzięki temu ustalimy jaki największy okrąg o środku 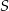 się w nim mieści).
się w nim mieści).
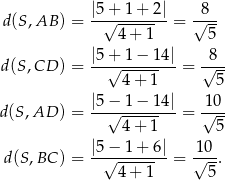
Mogliśmy też oczywiście zauważyć, że 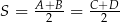 jest środkiem symetrii równoległoboku
jest środkiem symetrii równoległoboku 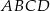 i obliczyć tylko dwie z tych odległości. Widzimy teraz, że promień największego okręgu zawartego w równoległoboku
i obliczyć tylko dwie z tych odległości. Widzimy teraz, że promień największego okręgu zawartego w równoległoboku 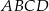 jest równy
jest równy 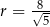 i równanie tego okręgu ma postać
i równanie tego okręgu ma postać
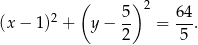
Odpowiedź: