/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Różne

Zadanie nr 8749244

Dany jest okrąg o równaniu 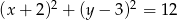2 2 (x+ 2) + (y− 3) = 12 oraz punkt 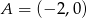A = (−2 ,0) . Napisz równanie symetralnej odcinka, którego końcami są dany punkt 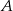A i środek 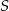S danego okręgu.

Wersja PDF

Rozwiązanie

PIC

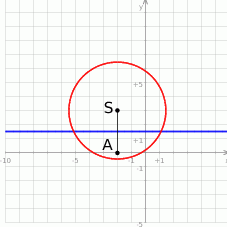
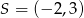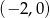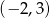Środek podanego okręgu to punkt S = (− 2,3) . Musimy zatem napisać równanie symetralnej odcinka o końcach (− 2,0) i (− 2,3) . Środek tego odcinka ma współrzędne 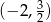(− 2, 3 ) 2 . Ponieważ odcinek ten jest pionowy, to szukana symetralna jest poziomą prostą i ma przechodzić przez punkt 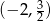3 (− 2,2 ) . Jest to zatem prosta 3 y = 2 .  
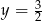Odpowiedź: y = 32

Wersja PDF