Zadanie nr 8906304

Dane są ﬁgury:

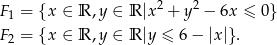
2 2 F1 = {x ∈ R,y ∈ R|x + y − 6x ≤ 0} F2 = {x ∈ R,y ∈ R|y ≤ 6 − |x|}.

Narysuj ﬁ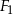gury i 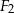oraz wyznacz ﬁgurę .
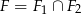Oblicz pole ﬁgury

Wersja PDF

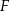
Rozwiązanie

Ponieważ

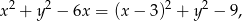
2 2 2 2 x + y − 6x = (x − 3) + y − 9,

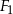ﬁgura F 1 jest wnętrzem okręgu o środku 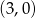(3 ,0) i promieniu 3.

Druga ﬁgura to wszystko co znajduje się pod wykresem funkcji 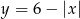y = 6− |x| . Funkcja ta to 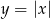y = |x| odbita względem os 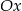i przesunięta o 6 jednostek w górę.

Bez trudu teraz rysujemy obie ﬁgury i zaznaczamy część wspólną.

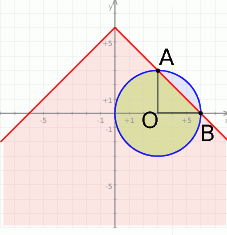
Odpowiedź: Rysunek
Z rysunku widać, że funkcja 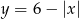przecina okrąg w punktach 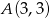i 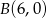. Jeżeli chcielibyśmy to wyliczyć a nie odczytywać z wykresu, to wystarczy wziąć prawy kawałek wykresu funkcji 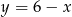i wstawić do równania okręgu. Zaznaczony trójkąt 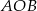jest prostokątny, więc łuk 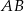to dokładnie 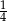całego okręgu. Zatem wycinek kołowy który mu odpowiada ma pole 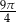. Aby otrzymać pole odcinka kołowego opartego na tym łuku musimy odjąć pole trójkąta 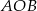. Zatem pole odcinka (czyli 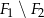) to
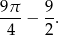
$9π 9 ---− -. 4 2$

Wyliczone pole to dokładnie tyle ile trzeba odjąć od pola całego koła aby otrzymać pole .

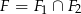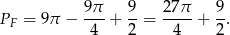
$9π 9 27π 9 PF = 9 π − --- + --= ---- + --. 4 2 4 2$

Odpowiedź: