/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Różne

Zadanie nr 9471231

Dodaj do ulubionych
Dodaj do rozwiązanych

O ile procent pole koła o promieniu długości 8 jest większe od pola koła wyznaczonego przez okrąg o równaniu 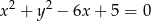x2 + y2 − 6x + 5 = 0 .

Rozwiązanie

Wyznaczamy długość promienia z równania okręgu

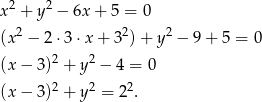
2 2 x + y − 6x + 5 = 0 (x2 − 2 ⋅3⋅ x+ 32)+ y 2 − 9 + 5 = 0 2 2 (x − 3) + y − 4 = 0 (x − 3)2 + y2 = 22.

Jest to więc okrąg o promieniu 2. Oznaczmy przez 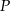P pole koła o promieniu 8, a przez 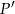′ P pole koła o promieniu 2. Mamy zatem

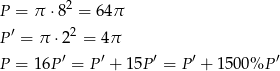
2 P = π ⋅8 = 64π P′ = π ⋅2 2 = 4π ′ ′ ′ ′ ′ P = 1 6P = P + 15P = P + 1500%P

 
Odpowiedź: 1500%

Wersja PDF