/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Różne

Zadanie nr 9473537

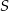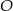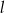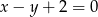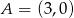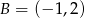Środek S okręgu O należy do prostej l o równaniu x− y+ 2 = 0 . Punkty A = (3,0) i B = (− 1,2) należą do tego okręgu.

  • Wyznacz równanie okręgu O .
  • Wyznacz współrzędne takiego punktu 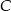C należącego do okręgu 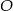O , że
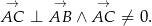
    → → → AC ⊥ AB ∧ AC ⁄= 0.
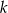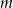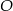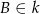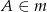  • Wyznacz równania stycznych k i m do okręgu O takich, że B ∈ k i A ∈ m oraz oblicz tangens jednego z kątów, pod jakim przecinają się te styczne.
Wersja PDF

Rozwiązanie

Zaczynamy oczywiście od szkicowego rysunku.

PIC

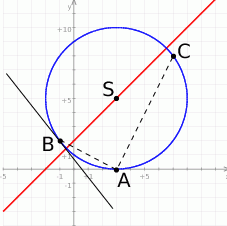
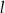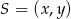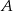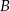  • Wyznaczmy najpierw środek okręgu. Aby to zrobić musimy znaleźć na podanej prostej l punkt S = (x,y) , który jest równo odległy od punktów A i B . Punkt ma leżeć na prostej 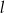l , zatem y = x + 2 .
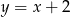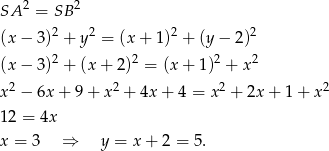
    2 2 SA = SB (x − 3)2 + y2 = (x + 1)2 + (y − 2)2 2 2 2 2 (x − 3) + (x + 2) = (x + 1) + x x2 − 6x + 9 + x2 + 4x + 4 = x2 + 2x + 1 + x2 12 = 4x x = 3 ⇒ y = x + 2 = 5.

    Zatem 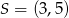S = (3,5) . Policzmy jeszcze promień okręgu O .

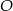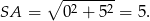
    ∘ ------- SA = 02 + 52 = 5.

     
    O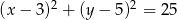dpowiedź: (x − 3)2 + (y − 5)2 = 25

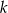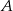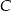  • Napiszemy równanie prostej k przechodzącej przez punkt A i prostopadłej do wektora AB = [− 4,2] . Szukany punkt C będzie punktem wspólnym tej prostej z okręgiem. Korzystamy ze wzoru na równanie prostej prostopadłej do wektora →v = [p,q] i przechodzącej przez punkt (x ,y ) 0 0
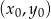
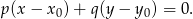
    p (x− x0)+ q(y− y0) = 0.

    W naszej sytuacji mamy

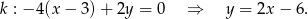
    k : − 4 (x− 3)+ 2y = 0 ⇒ y = 2x − 6.

    Szukamy punktu wspólnego z okręgiem

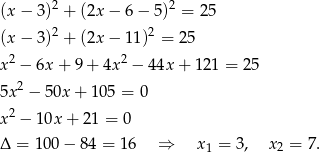
    (x− 3)2 + (2x− 6− 5)2 = 25 (x− 3)2 + (2x− 11)2 = 25 2 2 x − 6x + 9+ 4x − 44x + 12 1 = 25 5x2 − 50x + 105 = 0 x2 − 10x + 21 = 0 Δ = 1 00− 84 = 16 ⇒ x = 3, x = 7. 1 2

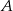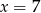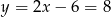    Pierwsze rozwiązanie daje nam punkt A , zatem x = 7 i y = 2x − 6 = 8 .  
    Odpowiedź: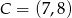 C = (7,8)

  • Styczną do okręgu w punkcie 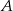A jest oś 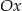Ox – łatwo sprawdzić, że ma ona tylko jeden punkt wspólny z okręgiem. Pozostało wyliczyć równanie drugiej stycznej. Napiszemy je jako równanie prostej przechodzącej przez punkt 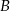B i prostopadłej do wektora BS = [4,3] .
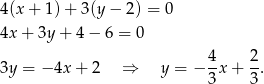
    4(x+ 1)+ 3(y− 2) = 0 4x+ 3y + 4− 6 = 0 4 2 3y = − 4x + 2 ⇒ y = − -x + -. 3 3

    Szukany tangens kąt przecięcia tej prostej z osią 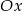Ox to po prostu współczynnik kierunkowy tej prostej.  
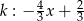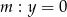    Odpowiedź: k : − 4x + 2 3 3 , m : y = 0 , 4 tg = − 3

Wersja PDF