Zadanie nr 7483522
Dana jest funkcja 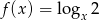 .
.
- Określ dziedzinę funkcji
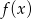 .
. - Naszkicuj wykres funkcji
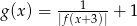 .
. - Odczytaj z wykresu maksymalne przedziały monotoniczności funkcji
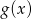 .
.
Rozwiązanie
- Ze względu na
 w podstawie logarytmu musi być
w podstawie logarytmu musi być 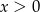 i
i 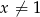 .
.
Odpowiedź: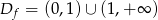
- Zauważmy, że
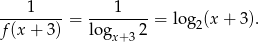
Zatem
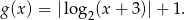
Wykres funkcji
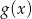 powstaje z wykresu funkcji
powstaje z wykresu funkcji 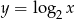 przez przesunięcie o 3 jednostki w lewo, potem odbicie części poniżej osi
przez przesunięcie o 3 jednostki w lewo, potem odbicie części poniżej osi 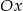 do góry, a na koniec przesunięcie wszystkiego o 1 jednostkę do góry.
do góry, a na koniec przesunięcie wszystkiego o 1 jednostkę do góry. 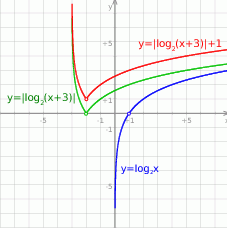
- Odczytujemy z wykresu.
Odpowiedź: Malejąca na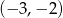 , rosnąca na
, rosnąca na