Zadanie nr 3509037
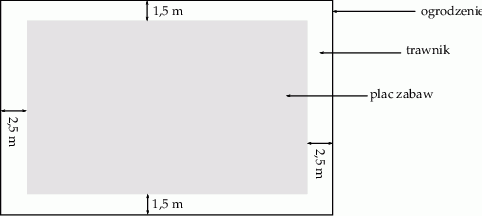
Należy zaprojektować wymiary prostokątnego placu zabaw, tak aby szerokość trawnika wzdłuż dłuższych brzegów placu była równa 1,5 m, a szerokość trawnika wzdłuż krótszych brzegów placu była równa 2,5 m (zobacz rysunek – plac zabaw zaznaczono kolorem szarym). Sam plac zabaw ma mieć powierzchnię 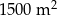 . Wyznacz takie wymiary placu zabaw, przy których powierzchnia placu wraz z trawnikami jest najmniejsza.
. Wyznacz takie wymiary placu zabaw, przy których powierzchnia placu wraz z trawnikami jest najmniejsza.
Rozwiązanie
Oznaczmy przez  długość krótszego boku placu zabaw. Wtedy dłuższy bok tego placu ma długość
długość krótszego boku placu zabaw. Wtedy dłuższy bok tego placu ma długość 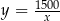 . Musimy teraz znaleźć najmniejszą wartość funkcji
. Musimy teraz znaleźć najmniejszą wartość funkcji
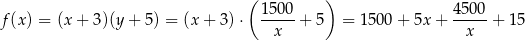
określonej dla 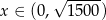 (bo
(bo  ma być krótszym bokiem placu zabaw). Liczymy pochodną
ma być krótszym bokiem placu zabaw). Liczymy pochodną
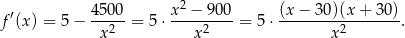
Widać teraz, że pochodna jest ujemna w przedziale 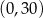 i dodatnia w przedziale
i dodatnia w przedziale 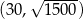 . To oznacza, że funkcja
. To oznacza, że funkcja 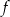 maleje w przedziale
maleje w przedziale 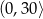 i rośnie w przedziale
i rośnie w przedziale 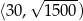 . W takim razie najmniejsze pole otrzymamy dla
. W takim razie najmniejsze pole otrzymamy dla 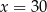 . Dłuższy bok placu zabaw ma wtedy długość
. Dłuższy bok placu zabaw ma wtedy długość
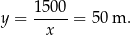
Odpowiedź: 30 m i 50 m.

