Zadanie nr 4648263
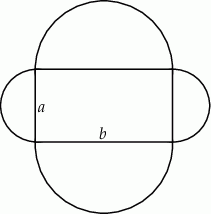
Na bokach prostokąta o obwodzie 16 cm opisano, jako na średnicach, półokręgi leżące na zewnątrz prostokąta. Zbadaj, dla jakich długości boków prostokąta, pole figury ograniczonej krzywą złożoną z tych czterech półokręgów jest najmniejsze. Oblicz to pole
Rozwiązanie
Naszkicujmy sobie opisaną sytuację i oznaczmy boki prostokąta przez  i
i 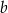 .
.
Wiemy, że 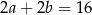 , czyli
, czyli 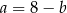 . Pole figury ograniczonej przez cztery dorysowane łuki jest równe sumie pól kół o średnicach
. Pole figury ograniczonej przez cztery dorysowane łuki jest równe sumie pól kół o średnicach  i
i 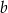 (bo mamy po dwie połówki takich kół) i pola prostokąta, czyli
(bo mamy po dwie połówki takich kół) i pola prostokąta, czyli
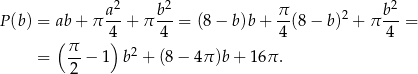
Pozostało wyznaczyć wartość 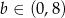 (bo
(bo 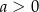 ), dla której wartość
), dla której wartość 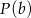 jest najmniejsza. Ponieważ wykresem funkcji
jest najmniejsza. Ponieważ wykresem funkcji 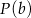 jest parabola o ramionach skierowanych do góry, więc przyjmuje ona wartość najmniejszą w wierzchołku paraboli, czyli w punkcie
jest parabola o ramionach skierowanych do góry, więc przyjmuje ona wartość najmniejszą w wierzchołku paraboli, czyli w punkcie
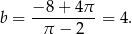
Mamy wtedy
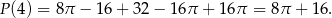
Odpowiedź: Boki: 4 cm i 4 cm, pole figury: