Zadanie nr 4825283
Bok kwadratu 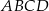 ma długość 1. Na bokach
ma długość 1. Na bokach 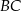 i
i 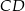 wybrano odpowiednio punkty
wybrano odpowiednio punkty 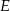 i
i 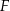 umieszczone tak, by
umieszczone tak, by 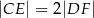 . Oblicz wartość
. Oblicz wartość 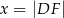 , dla której pole trójkąta
, dla której pole trójkąta 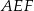 jest najmniejsze.
jest najmniejsze.
Rozwiązanie
Rozpoczynamy od rysunku
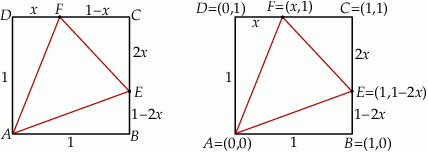
Sposób I
Pole trójkąta 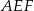 będzie najmniejsze jeżeli suma pól trójkątów prostokątnych
będzie najmniejsze jeżeli suma pól trójkątów prostokątnych 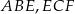 i
i 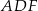 będzie największa. Szukamy zatem wartości największej funkcji
będzie największa. Szukamy zatem wartości największej funkcji
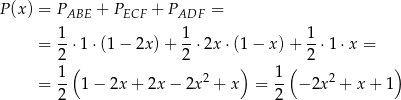
określonej dla 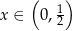 . Wykresem tej funkcji jest parabola o ramionach skierowanych w dół, więc największą wartość otrzymamy w wierzchołku, czyli dla
. Wykresem tej funkcji jest parabola o ramionach skierowanych w dół, więc największą wartość otrzymamy w wierzchołku, czyli dla
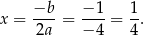
Na koniec pozostaje zauważyć, że otrzymana wartość  należy do dziedziny funkcji
należy do dziedziny funkcji 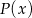 .
.
Sposób II
Dorysujmy na płaszczyźnie układ współrzędnych tak, aby 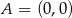 i
i 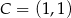 . Wtedy
. Wtedy 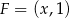 i
i 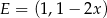 . Zatem ze wzoru na pole trójkąta o wierzchołkach
. Zatem ze wzoru na pole trójkąta o wierzchołkach 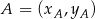 ,
, 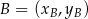 i
i 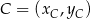 .
.
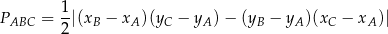
mamy
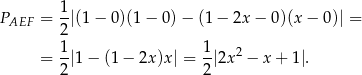
Ponieważ 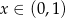 , więc
, więc
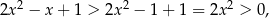
czyli wyrażenie pod wartością bezwzględną jest dodatnie i mamy
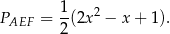
Wykresem tej funkcji jest parabola o ramionach skierowanych w górę, czyli największą wartość otrzymamy w wierzchołku, czyli dla
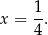
Jak poprzednio zauważamy, że otrzymana wartość  należy do dziedziny funkcji
należy do dziedziny funkcji 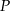 .
.
Odpowiedź: