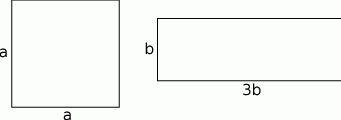
Drut o długości 28 cm należy podzielić na dwie części i z jednej zrobić kwadratową ramkę, a z drugiej ramkę prostokątną, której jeden bok jest trzy razy dłuższy od drugiego. Jak należy podzielić drut, jeżeli chcemy, aby suma pól otrzymanego kwadratu i prostokąta była najmniejsza?
Oznaczmy bok otrzymanego kwadratu przez 
, a boki otrzymanego prostokąta przez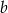 
i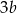 
.
Wiemy, że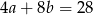 
, czyli 
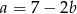. Chcemy znaleźć wartość 
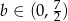(bo ma być 
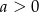), dla której funkcja
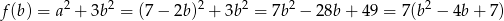
przyjmuje najmniejszą wartość. Wykresem tej funkcji jest parabola o ramionach skierowanych w górę, a więc wartość najmniejszą przyjmuje w wierzchołku paraboli, czyli w punkcie
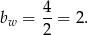
Odpowiedź: Optymalny podział: kwadrat o boku 3 cm i prostokąt 2 cm x 6 cm
Informacje
Zadania
Losowe zadanie
