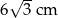Zadanie nr 7924898
Suma długości dwóch boków trójkąta jest równa 12 cm, a kąt między tymi bokami ma miarę 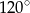 . Oblicz jakie powinny być długości boków tego trójkąta aby jego pole było największe.
. Oblicz jakie powinny być długości boków tego trójkąta aby jego pole było największe.
Rozwiązanie
Jeżeli oznaczymy długości boków, o których mowa w zadaniu, przez  i
i 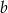 to mamy
to mamy 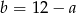 .
.
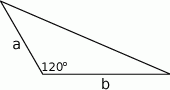
Ze wzoru na pole trójkąta mamy
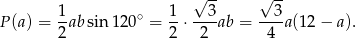
Pozostało znaleźć wartość 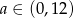 , dla której
, dla której 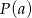 przyjmuje największą wartość. Ponieważ wykresem funkcji
przyjmuje największą wartość. Ponieważ wykresem funkcji 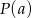 jest parabola o ramionach skierowanych w dół i miejscach zerowych 0 i 12, to przyjmuje ona wartość największą w wierzchołku paraboli, czyli w punkcie
jest parabola o ramionach skierowanych w dół i miejscach zerowych 0 i 12, to przyjmuje ona wartość największą w wierzchołku paraboli, czyli w punkcie 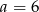 (środek odcinka łączącego miejsca zerowe).
(środek odcinka łączącego miejsca zerowe).
Długość trzeciego boku trójkąta możemy wyliczyć z twierdzenia cosinusów
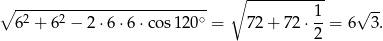
Odpowiedź: 6 cm, 6 cm i