Trapez prostokątny o podstawach długości 4 i 5 oraz kącie ostrym równym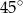 
obraca się wokół krótszej podstawy. Oblicz objętość otrzymanej bryły.
Jeżeli naszkicujemy sobie opisaną sytuację,
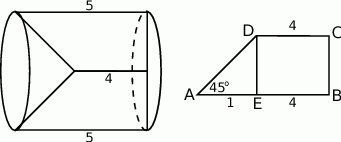
to widać, że po obrocie otrzymamy walec z wyciętym stożkiem. Zanim zaczniemy liczyć objętość tej bryły, wyznaczmy wysokość trapezu. Zauważmy, że trójkąt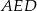 
jest równoramienny (jest to połówka kwadratu), zatem 
.
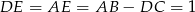W takim razie objętość całego walca to
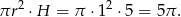
Od tej objętości trzeba odjąć objętość wyciętego stożka, czyli
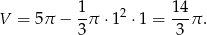
Odpowiedź: 
Informacje
Zadania
Losowe zadanie
