Zadanie nr 2926731
Trójkąt równoramienny o podstawie długości 6 cm i ramionach długości 5 cm obracamy wokół jednego z ramion. Otrzymaną w ten sposób bryłę dzielimy na dwa stożki. Podaj długość promienia podstawy i długość tworzącej każdego z tych stożków.
Rozwiązanie
Zaczynamy od schematycznego rysunku – rysujemy przekrój osiowy otrzymanej bryły.
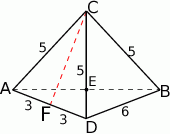
Na rysunku bok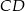 
jest bokiem, wokół którego obraca się trójkąt 
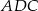. Trójkąty 
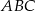i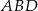 
są przekrojami osiowymi utworzonych stożków.
Z rysunku jest jasne, że tworzące otrzymanych stożków mają długość 5 cm i 6 cm. Promień podstawy tych stożków to dokładnie wysokość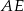 
trójkąta 
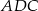. Zanim ją obliczymy, obliczmy najpierw wysokość 
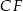. Liczymy ją z trójkąta prostokątnego 
.
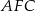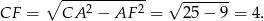
Możemy teraz napisać dwa wzory na pole trójkąta.
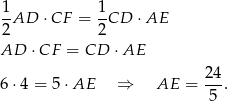
Odpowiedź: Promień podstawy: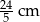 
, tworzące: 5 cm i 6 cm
