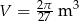/Szkoła średnia/Geometria/Stereometria/Inne bryły/Obrotowe

Zadanie nr 6882854

Dodaj do ulubionych
Dodaj do rozwiązanych

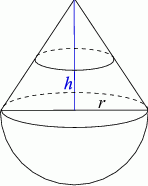
Kapsuła lądownika ma kształt stożka zakończonego w podstawie półkulą o tym samym promieniu co promień podstawy stożka. Wysokość stożka jest o 1 m większa niż promień półkuli. Objętość stożka stanowi 23 objętości całej kapsuły. Oblicz objętość kapsuły lądownika.

Rozwiązanie

Na początku zróbmy rysunek.

PIC

Objętość kapsuły jest sumą objętości stożka i połowy kuli, czyli jest równa:

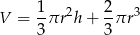
V = 1πr2h + 2πr 3 3 3

Korzystając z zależności 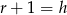r + 1 = h , otrzymujemy

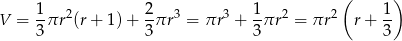
( ) V = 1-πr2(r + 1) + 2-πr3 = πr 3 + 1πr 2 = πr 2 r+ 1- 3 3 3 3

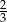Pozostało wyliczyć r . Zrobimy to korzystając z informacji, że objętość stożka stanowi 2 3 objętości całej kapsuły.

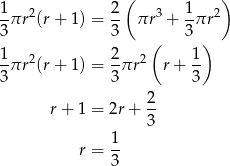
( ) 1- 2 2- 3 1- 2 3πr (r+ 1) = 3 πr + 3 πr ( ) 1πr 2(r+ 1) = 2-πr2 r + 1- 3 3 3 2 r+ 1 = 2r + -- 3 r = 1- 3

Stąd 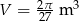V = 22π7-m 3 .  
Odpowiedź: V = 2π-m 3 27

Wersja PDF