Zadanie nr 1483495
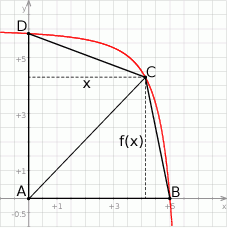
Na rysunku poniżej przedstawiono fragment wykresu funkcji 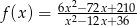 określonej dla
określonej dla 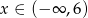 . Wykres ten przecina osie
. Wykres ten przecina osie 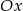 i
i 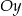 odpowiednio w punktach
odpowiednio w punktach 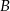 i
i 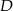 , a punkt
, a punkt 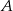 jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty
jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty 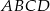 , w których punkt
, w których punkt 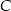 leży na wykresie funkcji
leży na wykresie funkcji 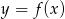 pomiędzy punktami
pomiędzy punktami 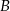 i
i 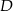 .
.
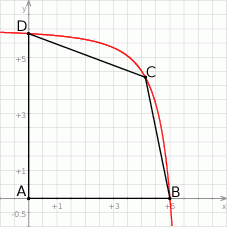
Oblicz pierwszą współrzędną wierzchołka 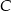 tego z rozpatrywanych czworokątów, którego pole jest największe.
tego z rozpatrywanych czworokątów, którego pole jest największe.
Rozwiązanie
Wyznaczmy najpierw współrzędne punktów 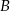 i
i 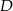 .
.
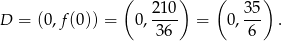
Aby wyznaczyć współrzędne punktu 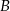 rozwiązujemy równanie
rozwiązujemy równanie
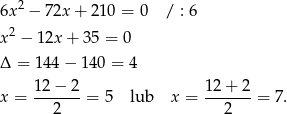
Ze względu na podaną dziedzinę funkcji mamy 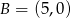 .
.
Aby obliczyć pole czworokąta 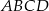 dzielimy go na 2 trójkąty przekątną
dzielimy go na 2 trójkąty przekątną 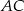 .
.
Jeżeli 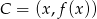 , to interesujące nas pole jest równe
, to interesujące nas pole jest równe
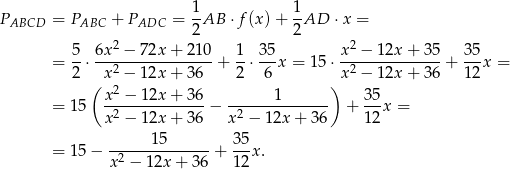
Liczymy pochodną tej funkcji.
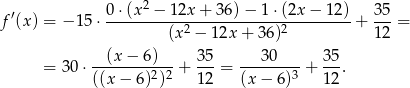
Sprawdzamy teraz kiedy pochodna jest równa 0.
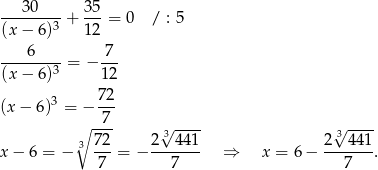
Zauważmy jeszcze, że funkcja 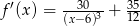 jest malejąca w przedziale
jest malejąca w przedziale 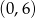 (bo
(bo 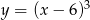 jest rosnąca), więc pochodna w punkcie
jest rosnąca), więc pochodna w punkcie 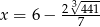 zmienia znak z dodatniego na ujemny. To oznacza, że w tym punkcie funkcja
zmienia znak z dodatniego na ujemny. To oznacza, że w tym punkcie funkcja 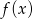 ma maksimum i jest to szukana wartość pierwszej współrzędnej wierzchołka
ma maksimum i jest to szukana wartość pierwszej współrzędnej wierzchołka 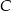 , dla której pole czworokąta
, dla której pole czworokąta 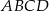 jest największe.
jest największe.
Odpowiedź: