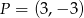Zadanie nr 2062444
Wyznacz współrzędne punktu 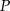 leżącego na wykresie funkcji
leżącego na wykresie funkcji 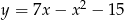 , dla którego suma odległości od osi układu współrzędnych jest najmniejsza.
, dla którego suma odległości od osi układu współrzędnych jest najmniejsza.
Rozwiązanie
Możemy rozpocząć od szkicowego rysunku – parabola 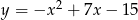 ma wierzchołek w punkcie
ma wierzchołek w punkcie
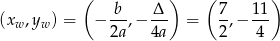
i ma ramiona skierowane w dół.
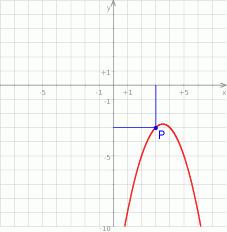
Ponieważ 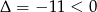 parabola znajduje się w całości pod osią
parabola znajduje się w całości pod osią 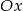 i suma odległości punktu
i suma odległości punktu 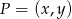 tej paraboli od osi układu jest równa
tej paraboli od osi układu jest równa
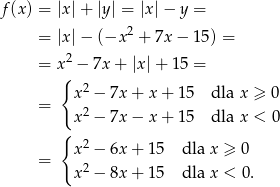
Pozostało wyznaczyć wartość najmniejszą tej funkcji. Pierwszy wzór osiąga najmniejszą wartość dla 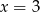 i jest ona równa
i jest ona równa 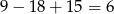 . Drugi wzór osiąga najmniejszą wartość dla
. Drugi wzór osiąga najmniejszą wartość dla 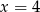 , ale punkt ten jest na prawo od
, ale punkt ten jest na prawo od 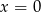 , więc funkcja ta jest malejąca na przedziale
, więc funkcja ta jest malejąca na przedziale 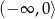 . Zatem najmniejsza możliwa wartość drugiego wzoru to wartość w
. Zatem najmniejsza możliwa wartość drugiego wzoru to wartość w 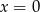 , czyli 15.
, czyli 15.
Podsumowując, najmniejsza wartość funkcji 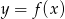 to
to 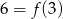 i odpowiada ona punktowi
i odpowiada ona punktowi
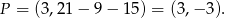
Odpowiedź: